
分析 (1)根据所给的函数式,代入自变量进行整理,观察分子和分母的特点,分子和分母同乘以一个代数式,使得分子和分母都变化成完全平方形式,开方合并同类型得到结果.
(2)先把原式中切转化成弦,利用两角和公式和整理后,运用诱导公式和二倍角公式化简整理求得答案.
解答 解:(1)∵f(x)=$\sqrt{\frac{1-x}{1+x}}$,α∈($\frac{π}{2}$,π),
∴f(cosα)+f(-cosα)=$\sqrt{\frac{1-cosα}{1+cosα}}$+$\sqrt{\frac{1+cosα}{1-cosα}}$=$\sqrt{\frac{(1-cosα)^{2}}{si{n}^{2}α}}$+$\sqrt{\frac{(1+cosα)^{2}}{si{n}^{2}α}}$=$\frac{|1-cosα|}{|sinα|}$+$\frac{|1+cosα|}{|sinα|}$=$\frac{2}{sinα}$;
(2)原式=sin50°•$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$=cos40°•$\frac{2sin40°}{cos10°}$=$\frac{sin80°}{cos10°}$=$\frac{cos10°}{cos10°}$=1.
点评 本题主要考查了三角函数的恒等变换及其化简求值,以及两角和公式,诱导公式和二倍角公式的化简求值.考查了学生对三角函数基础知识的综合运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | R | B. | {x|x≥5} | C. | {x|x<3} | D. | {x|3<x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}}$ | B. | $\frac{\overrightarrow a+\overrightarrow b}{{|{\overrightarrow a+\overrightarrow b}|}}$ | ||
| C. | $\frac{{|{\overrightarrow b}|\overrightarrow a-|{\overrightarrow a}|\overrightarrow b}}{{|{\overrightarrow a}|+|{\overrightarrow b}|}}$ | D. | $λ(\frac{\overrightarrow a}{{|{\overrightarrow a}|}}+\frac{\overrightarrow b}{{|{\overrightarrow b}|}})$,λ由$\overrightarrow{OM}$确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
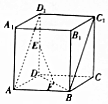 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com