Question

3．设由不等式组$\left\{\begin{array}{l}x-2y≥0\\ x+3y≥0\end{array}\right.$所确定的平面区域为Ω，若动点P（x，y）在圆x²+y²=1上运动，则动点P落在区域Ω内的概率为$\frac{1}{8}$，若动点P（x，y）在平面区域Ω内，且满足0≤x≤2，则函数f（x，y）=x-y的最大值为$\frac{8}{3}$．

Answer 1

分析 作出平面区域，计算区域边界的夹角，计算概率；移动目标函数得到最优解．

解答 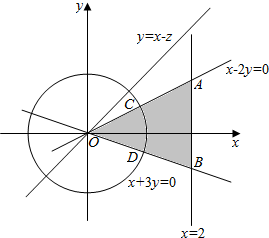解：作出平面区域如图所示：由直线的斜率可知tan∠AOX=$\frac{1}{2}$，tan∠BOX=$\frac{1}{3}$．
∴tan∠AOB=$\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2}×\frac{1}{3}}$=1．∴∠AOB=$\frac{π}{4}$．
∴当P在圆x²+y²=1上运动时，P点落在区域Ω内的概率为$\frac{\frac{π}{4}}{2π}$=$\frac{1}{8}$．
令z=x-y，则y=x-z，∴当z最大时，直线y=x-z在y轴上的截距最小．
由图可知当直线过点B时，截距最小，即z最大．
解方程组$\left\{\begin{array}{l}{x=2}\\{x+3y=0}\end{array}\right.$得x=2，y=-$\frac{2}{3}$．∴z的最大值为2-（-$\frac{2}{3}$）=$\frac{8}{3}$．
故答案为$\frac{1}{8}$，$\frac{8}{3}$．

点评 本题考查了简单的线性规划，几何概型的概率计算，作出平面区域是解题关键．