
分析 化双曲线方程为标准式,作出图形,由已知利用平面几何知识把|F1P|、|F2P|都用含有b得代数式表示,代入双曲线定义即可求得双曲线C的离心率.
解答 解:双曲线C:b2x2-a2y2=a2b2(a>0,b>0)化为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0).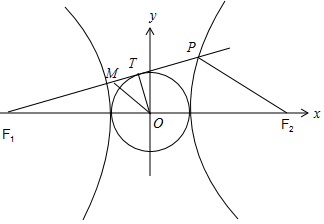
设双曲线的右焦点为F2,点M是线段F1P的中点,点O为坐标原点,
∴|F1T|=$\sqrt{|{F}_{1}O{|}^{2}-|OT{|}^{2}}$=$\sqrt{{c}^{2}-{a}^{2}}=b$.
∵$\overrightarrow{{F_1}T}=2\overrightarrow{TP}$,∴$|{F}_{1}P|=\frac{3}{2}|{F}_{1}T|=\frac{3}{2}b$,$|MT|=\frac{b}{4}$,$|{F}_{2}P|=2|OM|=2\sqrt{{a}^{2}+(\frac{1}{4}b)^{2}}$.
由双曲线定义,|F1P|-|F2P|=2a,即$\frac{3}{2}b-2\sqrt{{a}^{2}+(\frac{1}{4}b)^{2}}=2a$.
∴$\frac{3}{2}b-2a=2\sqrt{{a}^{2}+(\frac{1}{4}b)^{2}}$,两边平方并整理得:$\frac{b}{a}=3$.
则$\frac{{c}^{2}-{a}^{2}}{{a}^{2}}=9$,e2=10.
∴$e=\frac{c}{a}=\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 本题考查双曲线的简单性质,考查了计算求解能力,是中档题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
 《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用.如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输入的a值为$\frac{93}{32}$,则输出的m的值为( )
《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用.如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输入的a值为$\frac{93}{32}$,则输出的m的值为( )| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | 0 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 不低于120分(优秀) | 低于120分(非优秀) | |
| 男 | 12 | 21 |
| 女 | 11 | 19 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超过0.01的前提下认为“该班学生英语成绩优秀与性别有关” | |
| B. | 在犯错误的概率不超过0.05的前提下认为“该班学生英语成绩优秀与性别有关” | |
| C. | 没有90%以上的把握认为“该班学生英语成绩优秀与性别有关” | |
| D. | 有90%以上的把握认为“该班学生英语成绩优秀与性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $\frac{3\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y'=3sin2x' | B. | y'=3sin$\frac{x'}{2}$ | C. | y'=$\frac{1}{3}$sin2x' | D. | y'=$\frac{1}{3}sin\frac{x'}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com