
分析 根据对数函数的图象和性质,可判断①④⑤;根据抽象函数定义域的求法,可判断②;根据映射的定义,可判断③.
解答 ?解:当x=1时,ln(x-1)无意义,故①错误;
若函数f(x)的定义域为[-1,1],则由2x-1∈[-1,1]得:x∈[0,1],即函数f(2x-1)的定义域为[0,1],故②错误.
已知集合P={a,b},Q={-1,0,1},则映射f:P→Q中满足f(b)=0的映射共有3个,故③正确;.
若函数f(x)=log2(x2-2ax+1)的定义域为R,则x2-2ax+1>0恒成立,即△=4a2-4<0,故实数a的取值范围是(-1,1),故④正确.
函数f(x)=ex的图象关于直线y=x对称的函数解析式为y=lnx,故⑤错误;
故答案为:③④.
点评 本题以命题的真假判断与应用为载体,考查了对数函数的图象和性质,反函数,抽象函数的定义域,映射的定义等知识点,难度中档.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源:2017届江苏南通市如东县等高三10月联考数学试卷(解析版) 题型:解答题
已知函数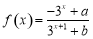 .
.
(1) 当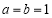 时,求满足
时,求满足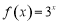 的
的 的取值;
的取值;
(2) 若函数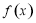 是定义在R上的奇函数
是定义在R上的奇函数
①存在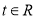 ,不等式
,不等式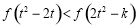 有解,求
有解,求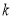 的取值范围;
的取值范围;
②若函数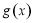 满足
满足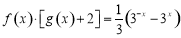 ,若对任意
,若对任意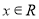 ,不等式
,不等式
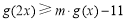 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
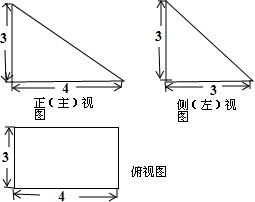 一个棱锥的三视图如图所示(所有三角形均为直角三角形),则这个棱锥的表面积为( )
一个棱锥的三视图如图所示(所有三角形均为直角三角形),则这个棱锥的表面积为( )| A. | 30+$\sqrt{2}$ | B. | 36 | C. | 30+6$\sqrt{2}$ | D. | 38 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | t≤-3或t≥-1 | B. | -3≤t≤-1 | C. | t≤1或t≥3 | D. | 1≤t≤3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤1 | B. | m≤-1 | C. | m>1 | D. | m>-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{25}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{25}-\frac{y^2}{9}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com