
���� ����A�ͺŵ��ӻ���Ͷ�Ž��Ϊx��Ԫ��1��x��9������B�ͺŵĵ��ӻ���Ͷ�Ž��Ϊ��10-x����Ԫ������ũ��õ��IJ���Ϊf��x����Ԫ���������$f��x��=\frac{2}{5}lnx+\frac{1}{10}��10-x��=\frac{2}{5}lnx-\frac{1}{10}x+1$�������õ�������˺��������ֵ���Ӷ��õ����䷽����������ֵ��
��� �⣺��A�ͺŵ��ӻ���Ͷ�Ž��Ϊx��Ԫ��1��x��9����
��B�ͺŵĵ��ӻ���Ͷ�Ž��Ϊ��10-x����Ԫ������ũ��õ��IJ���Ϊf��x����Ԫ��
�������$f��x��=\frac{2}{5}lnx+\frac{1}{10}��10-x��=\frac{2}{5}lnx-\frac{1}{10}x+1$����4�֣�
$f'��x��=\frac{2}{5x}-\frac{1}{10}=\frac{4-x}{10x}$����f'��x��=0��x=4��
��x�ʣ�1��4��ʱ��f'��x����0����x�ʣ�4��9����ʱ��f'��x����0��---------------------��8�֣�
���Ե�x=4ʱ��f��x��ȡ�����ֵ��$f{��x��_{max}}=\frac{2}{5}ln4-0.4+1��1.2$��---------��10�֣�
�ʳ���Ͷ��A��B�����ͺŵĵ��ӻ��Ľ��ֱ���4��Ԫ��6��Ԫ��
ũ��õ��IJ�����࣬��ಹ��Լ1.2��Ԫ��---------------------��12�֣�
���� ��С����Ҫ�������ʵ�����⽨����ѧģ�ͣ��Լ����ú�����������֪ʶ���ʵ��������������������õ�����������ֵ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
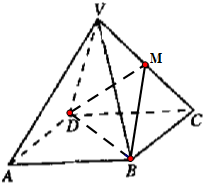 ��ͼ������V-ABCD�У�����ABCD�DZ߳�Ϊ2�������Σ������ĸ����涼�Dz��ⳤΪ$\sqrt{5}$�ĵ��������Σ�MΪVC���е㣮
��ͼ������V-ABCD�У�����ABCD�DZ߳�Ϊ2�������Σ������ĸ����涼�Dz��ⳤΪ$\sqrt{5}$�ĵ��������Σ�MΪVC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
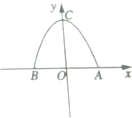 ��ͼ��������y=-x2+4��x����A��B���㣬����ΪC
��ͼ��������y=-x2+4��x����A��B���㣬����ΪC�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com