
分析 (Ⅰ)求导数,利用导数的正负求函数f(x)的单调区间;
(Ⅱ)即证明:$lnt-\frac{1}{t}<\frac{1}{2}t-\frac{3}{2t}$,即证:$lnt+\frac{1}{2t}-\frac{1}{2}t<0({t>1})$,设函数$g(t)=lnt+\frac{1}{2t}-\frac{1}{2}t,t>1$,则$g'(t)=-\frac{{{{({t-1})}^2}}}{{2{t^2}}}<0$,g(t)函数在(1,+∞)上为减函数,从而g(t)<g(1)=0,即可证明结论.
解答 (Ⅰ)解:若a∈(0,+∞),函数f(x)定义域为(0,1)∪(1,+∞),
由$f'(x)=\frac{{{x^2}-({2+a})x+1}}{{x{{({x-1})}^2}}}$,
∵△=(2+a)2-4>0,设f'(x)=0的两根为x1、x2(x1<x2),
解得${x_1}=\frac{{2+a-\sqrt{{a^2}+4a}}}{2},{x_2}=\frac{{2+a+\sqrt{{a^2}+4a}}}{2}$,
由x1+x2=2+a,x1x2=1,可得0<x1<1<x2,
当x∈(0,x1)∪(x2,+∞)时,f'(x)>0;
当x∈(x1,1)∪(1,x2)时,f'(x)<0.
故函数f(x)的单调增区间为$({0,\frac{{2+a-\sqrt{{a^2}+4a}}}{2}})$和$({\frac{{2+a+\sqrt{{a^2}+4a}}}{2},+∞})$,
单调递减区间为$({\frac{{2+a-\sqrt{{a^2}+4a}}}{2},1})$和$({1,\frac{{2+a+\sqrt{{a^2}+4a}}}{2}})$.…(6分)
(Ⅱ)证明:由(Ⅰ)知,t>1,函数f(x)的有极小值$f(t)=\frac{a}{t-1}+lnt-1$,而t2-(2+a)t+1=0,
故$a=\frac{{{{({t-1})}^2}}}{t}$,所以$f(t)=\frac{t-1}{t}+lnt-1=lnt-\frac{1}{t}$,即证明:$lnt-\frac{1}{t}<\frac{1}{2}t-\frac{3}{2t}$,
即证:$lnt+\frac{1}{2t}-\frac{1}{2}t<0({t>1})$,设函数$g(t)=lnt+\frac{1}{2t}-\frac{1}{2}t,t>1$,则$g'(t)=-\frac{{{{({t-1})}^2}}}{{2{t^2}}}<0$,
所以,g(t)函数在(1,+∞)上为减函数,从而g(t)<g(1)=0,
所以$f(t)<\frac{1}{2}t-\frac{3}{2t}$…(12分)
点评 本题考查导数知识的综合运用,考查函数的单调性、极值,考查学生分析解决问题的能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
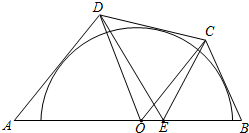 如图,已知凸四边形ABCD的顶点在一个圆周上,另一个圆的圆心O在AB上,且与四边形ABCD的其余三边相切.点E在边AB上,且AE=AD.
如图,已知凸四边形ABCD的顶点在一个圆周上,另一个圆的圆心O在AB上,且与四边形ABCD的其余三边相切.点E在边AB上,且AE=AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com