
| A�� | 12 | B�� | 8 | C�� | 7 | D�� | 6 |
���� ������ɵó鵽�ĺ��빹����3Ϊ�����30Ϊ����ĵȲ����У���ô˵Ȳ����е�ͨ�ʽΪan=3+��n-1��30=30n-27����721��30n-27��900�����������n�ĸ�������Ϊ�ó����ۣ�
��� �⣺��900��30=30��
��������ɵó鵽�ĺ��빹����3Ϊ�����30Ϊ����ĵȲ����У�
��721��30n-27��900��nΪ�������ɵ�25��n��30��
����C�������Ϊ30-25+1=6��
��ѡ��D��
���� ������Ҫ����Ȳ����е�ͨ�ʽ��ϵͳ�����Ķ���ͷ���������ϵͳ�����Ķ���ת��Ϊ�Ȳ������ǽ������Ĺؼ����Ƚϻ�����


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2��3} | B�� | {x|1��x��3} | C�� | {2��3} | D�� | {x|1��x��$\sqrt{10}$} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | -3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
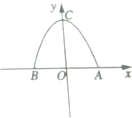 ��ͼ��������y=-x2+4��x����A��B���㣬����ΪC
��ͼ��������y=-x2+4��x����A��B���㣬����ΪC�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\sqrt{2}$��${2}^{\frac{e}{2}}$�� | B�� | ��0��2] | C�� | ��2��2${\;}^{\frac{e+2}{2}}$] | D�� | ��2${\;}^{\frac{3}{2}}$��2${\;}^{\frac{e+4}{4}}$�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com