
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),若四边形
是坐标原点),若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)离心率提供![]() 与
与![]() 的关系,四个顶点构成的四边形对角线互相垂直,列出等量关系求
的关系,四个顶点构成的四边形对角线互相垂直,列出等量关系求![]() ,
,![]() 的值;
的值;
(2)直线![]() 经过点
经过点![]() ,由直线点斜式方程设出直线
,由直线点斜式方程设出直线![]() 的方程,并设出直线
的方程,并设出直线![]() 与椭圆
与椭圆![]() 交点
交点![]() 、
、![]() 的坐标,联立方程,由韦达定理可表示出
的坐标,联立方程,由韦达定理可表示出![]() 的中点
的中点![]() 的坐标;由中点
的坐标;由中点![]() 的坐标可得直线
的坐标可得直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程,利用韦达定理可求
的方程,利用韦达定理可求![]() ,再利用点到直线距离公式可求点
,再利用点到直线距离公式可求点![]() 、
、![]() 到直线
到直线![]() 的距离,由四边形
的距离,由四边形![]() 的面积为
的面积为![]() 可列出等量关系,最后可求出直线
可列出等量关系,最后可求出直线![]() 的方程.
的方程.
解:(1)由题意可得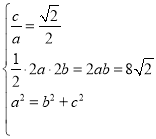 ,
,
解得![]() ,
,![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
联立 ,整理得
,整理得![]() ,
,
则![]() ,
,![]() ,
,
从而![]() ,故
,故![]() ,
,
直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
联立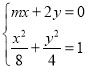 ,整理得
,整理得![]() ,
,
则![]() .
.
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离也为
的距离也为![]() ,
,
从而![]() .
.
∵点![]() ,
,![]() 在直线
在直线![]() 的两侧,
的两侧,
∴![]() ,
,
∴![]() ,则
,则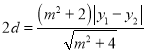 ,
,
∵![]() ,
,
∴![]() ,
,
则四边形![]() 的面积
的面积![]() ,
,
∵四边形![]() 的面积为
的面积为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
故直线![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】王老师在做折纸游戏,现有一张边长为1的正三角形纸片ABC,将点A翻折后恰好落在边BC上的点F处,折痕为DE,设![]() ,
,![]() .
.
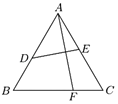
(1)求x、y满足的关系式;
(2)求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 在对角线
在对角线![]() 上,过点
上,过点![]() 作垂直于
作垂直于![]() 的平面
的平面![]() ,记平面
,记平面![]() 截正方体得到的截面多边形(含三角形)的周长为
截正方体得到的截面多边形(含三角形)的周长为![]() ,设
,设![]() ,
,![]() .
.
(1)下列说法中,正确的编号为______.
①截面多边形可能为六边形;②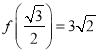 ;③函数
;③函数![]() 的图象关于
的图象关于![]() 对称.
对称.
(2)当![]() 时,三棱锥
时,三棱锥![]() 的外接球的表面积为______.
的外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,线段
的上、下顶点,线段![]() 长为
长为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
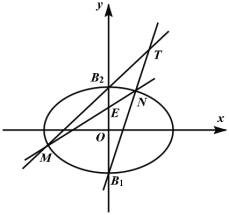
(1)求该椭圆的方程;
(2)已知过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
①若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标;
的坐标;
②求证点![]() 在一条定直线上,并写出该直线方程.
在一条定直线上,并写出该直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前
的前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,设
,设![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() .在以原点为极点,
.在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在北宋1084年第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰.某图书馆中正好有这十本书现在小明同学从这十本书中任借两本阅读,那么他取到的书的书名中有“算”字的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国全面二孩政策已于2016年1月1日起正式实施.国家统计局发布的数据显示,从2012年到2017年,中国的人口自然增长率变化始终不大,在5‰上下波动(如图).

为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何,统计部门按年龄分为9组,每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数,得到下表:
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)设每个年龄区间的中间值为![]() ,有意愿数为
,有意愿数为![]() ,求样本数据的线性回归直线方程,并求该模型的相关系数
,求样本数据的线性回归直线方程,并求该模型的相关系数![]() (结果保留两位小数);
(结果保留两位小数);
(2)从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
(参考数据和公式: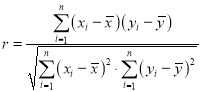 ,
,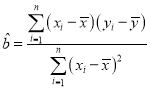 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com