
【题目】正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 在对角线
在对角线![]() 上,过点
上,过点![]() 作垂直于
作垂直于![]() 的平面
的平面![]() ,记平面
,记平面![]() 截正方体得到的截面多边形(含三角形)的周长为
截正方体得到的截面多边形(含三角形)的周长为![]() ,设
,设![]() ,
,![]() .
.
(1)下列说法中,正确的编号为______.
①截面多边形可能为六边形;②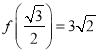 ;③函数
;③函数![]() 的图象关于
的图象关于![]() 对称.
对称.
(2)当![]() 时,三棱锥
时,三棱锥![]() 的外接球的表面积为______.
的外接球的表面积为______.
【答案】①③ ![]()
【解析】
(1)运用正方体的对角线的性质和对称性,得到截面为正三角性或正六边形,计算即可得到结论;
(2)确定外接圆的球心在OP上,运用勾股定理求得球的半径,利用表面积公式,即可求解.
(1)正方体![]() 的棱长为2,可得对角线长为
的棱长为2,可得对角线长为![]() ,
,
对于①中,由线面垂直的判定定理和性质,可得![]() 平面
平面![]() ,
,
当截面经过![]() 中点时,此时得到的截面垂直与
中点时,此时得到的截面垂直与![]() ,且为正六边形,所以截面多边形可能为六边形,所以是正确的;
,且为正六边形,所以截面多边形可能为六边形,所以是正确的;
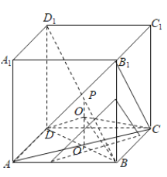
对于②中,当![]() 时,可得截面为等边
时,可得截面为等边![]() ,如图所示,
,如图所示,
设等边![]() 的边长为
的边长为![]() ,可得
,可得![]() ,
,![]()
在直角![]() 中,可得
中,可得![]() ,即
,即![]() ,
,
解得![]() ,所以截面
,所以截面![]() 的周长
的周长![]() ,所以②不正确;
,所以②不正确;

③根据正方体的对称性,可得函数![]() 的图象关于
的图象关于![]() 对称,所以是正确的;
对称,所以是正确的;
(2)由正方体![]() 的棱长为2,可得对角线长为
的棱长为2,可得对角线长为![]() ,
,
当![]() 时,可得点
时,可得点![]() 恰为对角线
恰为对角线![]() 的中点,则P在底面上的射影为AC的中点
的中点,则P在底面上的射影为AC的中点![]() ,
,
由球的性质,可得球心![]() 在
在![]() 上,
上,
设球的半径为![]() ,可得
,可得![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以三棱锥![]() 为外接球的表面积为
为外接球的表面积为![]() .
.
故答案为:①③,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某单位为了更好地应对新型冠状病毒肺炎疫情,对单位的职工进行防疫知识培训,所有职工选择网络在线培训和线下培训中的一种方案进行培训.随机抽取了140人的培训成绩,统计发现样本中40个成绩来自线下培训职工,其余来自在线培训的职工,并得到如下统计图表:
线下培训茎叶图在线培训直方图
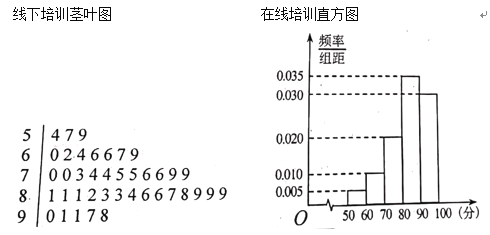
(1)得分90分及以上为成绩优秀,完成下边列联表,并判断是否有![]() 的把握认为成绩优秀与培训方式有关?
的把握认为成绩优秀与培训方式有关?
优秀 | 非优秀 | 合计 | |
线下培训 | |||
在线培训 | |||
合计 |
(2)成绩低于60分为不合格.在样本的不合格个体中随机再抽取3个,其中在线培训个数是![]() ,求
,求![]() 分布列与数学期望.
分布列与数学期望.
附: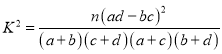 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学各有![]() 张卡片,现以投掷一枚骰子的形式进行游戏,当掷出奇数点时.甲赢得乙卡片一张,当掷出偶数点时,乙赢得甲卡片一张.规定投掷的次数达到
张卡片,现以投掷一枚骰子的形式进行游戏,当掷出奇数点时.甲赢得乙卡片一张,当掷出偶数点时,乙赢得甲卡片一张.规定投掷的次数达到![]() 次,或在此之前某入赢得对方所有卡片时,游戏终止.
次,或在此之前某入赢得对方所有卡片时,游戏终止.
(1)设![]() 表示游戏终止时投掷的次数,求
表示游戏终止时投掷的次数,求![]() 的分布列及期望;
的分布列及期望;
(2)求在投掷![]() 次游戏才结束的条件下,甲、乙没有分出胜负的概率.
次游戏才结束的条件下,甲、乙没有分出胜负的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为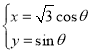 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换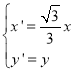 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴,建立极坐标系.设
轴的正半轴为极轴,建立极坐标系.设![]() 点的极坐标为
点的极坐标为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】恩格尔系数是食品支出总额占个人消费支出总额的比重,其数值越小说明生活富裕程度越高.统计改革开放40年来我国历年城镇和农村居民家庭恩格尔系数,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
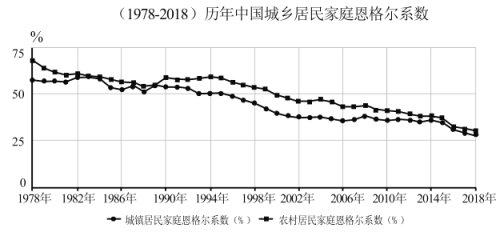
A.城镇居民家庭生活富裕程度不低于农村居民家庭
B.随着改革开放的不断深入,城镇和农村居民家庭生活富裕程度越来越高
C.1996年开始城镇和农村居民家庭恩格尔系数都低于50%
D.随着城乡一体化进程的推进,城镇和农村居民家庭生活富裕程度差别越来越小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),若四边形
是坐标原点),若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将6名党员干部分配到4个贫困村驻村扶贫,每个贫困村至少分配1名党员干部,则不同的分配方案共有( )
A.2640种B.4800种C.1560种D.7200种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com