
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最小值;
的最小值;
(2)若函数![]() 在
在![]() 上存在极值点,求实数
上存在极值点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求导后可得![]() ,令
,令![]() ,利用导数可知函数
,利用导数可知函数![]() 恒成立,由此可得函数
恒成立,由此可得函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,进而得到最小值;
上单调递增,进而得到最小值;
(2)分![]() 及
及![]() 讨论,当
讨论,当![]() 时,
时,![]() 无极值;当
无极值;当![]() 时,利用导数可知满足题意,进而得出结论.
时,利用导数可知满足题意,进而得出结论.
解:(1)由已知得当![]() 时,
时,
![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
易知函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,
,
则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
因此![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() .
.
(2)![]()
令![]() .
.
①当![]() 时,
时,![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() ,
,
此时![]() 在
在![]() 单调递増,所以函数
单调递増,所以函数![]() 无极值.
无极值.
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上存在唯一零点,设为
上存在唯一零点,设为![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
所以当![]() 时,函数
时,函数![]() 在
在![]() 上存在极值点
上存在极值点![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】王老师在做折纸游戏,现有一张边长为1的正三角形纸片ABC,将点A翻折后恰好落在边BC上的点F处,折痕为DE,设![]() ,
,![]() .
.
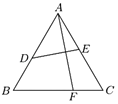
(1)求x、y满足的关系式;
(2)求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 至多只有一个公共点,求实数
至多只有一个公共点,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 的中点为
的中点为![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率为
的焦点,离心率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 在对角线
在对角线![]() 上,过点
上,过点![]() 作垂直于
作垂直于![]() 的平面
的平面![]() ,记平面
,记平面![]() 截正方体得到的截面多边形(含三角形)的周长为
截正方体得到的截面多边形(含三角形)的周长为![]() ,设
,设![]() ,
,![]() .
.
(1)下列说法中,正确的编号为______.
①截面多边形可能为六边形;②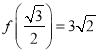 ;③函数
;③函数![]() 的图象关于
的图象关于![]() 对称.
对称.
(2)当![]() 时,三棱锥
时,三棱锥![]() 的外接球的表面积为______.
的外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,线段
的上、下顶点,线段![]() 长为
长为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
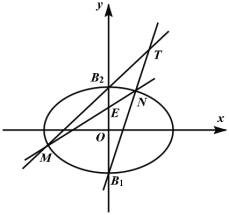
(1)求该椭圆的方程;
(2)已知过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
①若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标;
的坐标;
②求证点![]() 在一条定直线上,并写出该直线方程.
在一条定直线上,并写出该直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在北宋1084年第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰.某图书馆中正好有这十本书现在小明同学从这十本书中任借两本阅读,那么他取到的书的书名中有“算”字的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com