
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,线段
的上、下顶点,线段![]() 长为
长为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
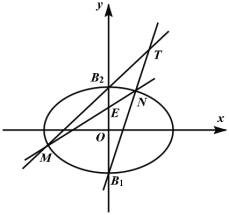
(1)求该椭圆的方程;
(2)已知过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
①若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标;
的坐标;
②求证点![]() 在一条定直线上,并写出该直线方程.
在一条定直线上,并写出该直线方程.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②证明详见解析,直线方程为
;②证明详见解析,直线方程为![]() .
.
【解析】
(1)由短轴长及离心率和![]() 之间的关系求出
之间的关系求出![]() 的值,进而求出椭圆的方程;
的值,进而求出椭圆的方程;
(2)①由(1)可得![]() 的坐标,设直线
的坐标,设直线![]() 的方程,与椭圆联立求出
的方程,与椭圆联立求出![]() 的坐标,求出直线
的坐标,求出直线![]() ,再求两条直线的交点
,再求两条直线的交点![]() 的坐标;
的坐标;
②设直线![]() 的方程,与椭圆联立求出两根之和及两根之积,求出直线
的方程,与椭圆联立求出两根之和及两根之积,求出直线![]() ,再求两条直线的交点
,再求两条直线的交点![]() 的坐标
的坐标![]() 与
与![]() 的坐标的关系,由两根之和及两根之积代入可得
的坐标的关系,由两根之和及两根之积代入可得![]() ,解得
,解得![]() ,即
,即![]() 在直线
在直线![]() 上.
上.
(1)![]() ,
,![]() ,
,
又![]() ,解得:
,解得:![]() ,
,
![]() 椭圆的方程为
椭圆的方程为![]() ;
;
(2)①由(1)可得:![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
直线![]() 方程为
方程为![]() ,代入椭圆方程整理得:
,代入椭圆方程整理得:![]()
解得:![]() ,
,![]() ,
,![]() ,
,
![]() 直线
直线![]() 方程为:
方程为: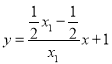 ;直线
;直线![]() 方程为
方程为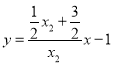 ,
,
由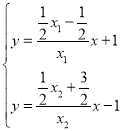 得:
得:![]() ,
,![]() ,
,![]() ;
;
②设![]() ,
,![]() ,
,
由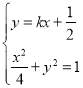 整理可得:
整理可得:![]() ,
,
则![]() ,
,![]() ,
,
![]() 直线
直线![]() 方程为
方程为![]() ;直线
;直线![]() 方程为
方程为![]() ;
;
![]() 由
由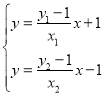 得:
得:![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,

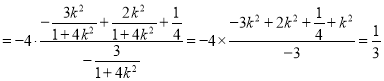 ,
,
![]() ,
,![]() 在定直线
在定直线![]() 上.
上.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为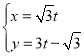 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为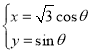 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换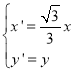 得到曲线
得到曲线![]() ,以原点为极点,
,以原点为极点,![]() 轴的正半轴为极轴,建立极坐标系.设
轴的正半轴为极轴,建立极坐标系.设![]() 点的极坐标为
点的极坐标为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】恩格尔系数是食品支出总额占个人消费支出总额的比重,其数值越小说明生活富裕程度越高.统计改革开放40年来我国历年城镇和农村居民家庭恩格尔系数,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
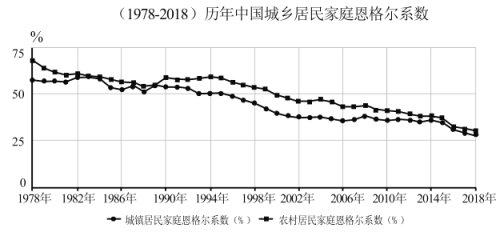
A.城镇居民家庭生活富裕程度不低于农村居民家庭
B.随着改革开放的不断深入,城镇和农村居民家庭生活富裕程度越来越高
C.1996年开始城镇和农村居民家庭恩格尔系数都低于50%
D.随着城乡一体化进程的推进,城镇和农村居民家庭生活富裕程度差别越来越小
查看答案和解析>>
科目:高中数学 来源: 题型:
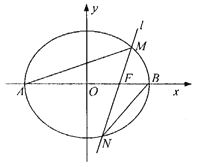
【题目】如图,已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,过右焦点
的左、右顶点,过右焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),若四边形
是坐标原点),若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. “![]() 在
在![]() 处有极值”是“
处有极值”是“![]() ”的充要条件
”的充要条件
D. 命题“若函数![]() 有零点,则“
有零点,则“![]() 或
或![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com