
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)
【解析】试题分析:(1)先根据导数几何意义得![]() ,解得实数
,解得实数![]() 的值;(2)设
的值;(2)设![]() ,构造函数
,构造函数![]() ,则转化为
,则转化为![]() 在
在![]() 上为增函数,即得
上为增函数,即得![]() 在
在![]() 上恒成立,参变分离得
上恒成立,参变分离得![]() ,最后根据二次函数最值求实数
,最后根据二次函数最值求实数![]() 的取值范围;(3)先化简不等式,并构造函数
的取值范围;(3)先化简不等式,并构造函数![]() ,求导数,按导函数零点与定义区间大小关系讨论函数单调性,根据单调性确定函数最小值,根据最小值小于零解得实数
,求导数,按导函数零点与定义区间大小关系讨论函数单调性,根据单调性确定函数最小值,根据最小值小于零解得实数![]() 的取值范围.
的取值范围.
试题解析:解:(1)由![]() ,得
,得![]() .
.
由题意, ![]() ,所以
,所以![]() .
.
(2)![]() .
.
因为对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,设
恒成立,设![]() ,则
,则![]() 即
即![]() 恒成立.
恒成立.
问题等价于函数![]() ,
,
即![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() 在
在![]() 上恒成立.即
上恒成立.即![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
(3)不等式![]() 等价于
等价于![]() ,整理得
,整理得![]() .构造函数
.构造函数![]() ,
,
由题意知,在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() .
.
![]() .
.
因为![]() ,所以
,所以![]() ,令
,令![]() ,得
,得![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增.只需
上单调递增.只需![]() ,解得
,解得![]() .
.
②当![]() 即
即![]() 时,
时, ![]() 在
在![]() 处取最小值.
处取最小值.
令![]() 即
即![]() ,可得
,可得![]() .
.
令![]() ,即
,即![]() ,不等式
,不等式![]() 可化为
可化为![]() .
.
因为![]() ,所以不等式左端大于1,右端小于等于1,所以不等式不能成立.
,所以不等式左端大于1,右端小于等于1,所以不等式不能成立.
③当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,只需
上单调递减,只需![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是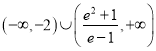 .
.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. “![]() ,若
,若![]() ,则
,则![]() 且
且![]() ”是真命题
”是真命题
B. 在同一坐标系中,函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称.
轴对称.
C. 命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,都有
,都有![]() ”
”
D. ![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,公差d>0,其前n项和为Sn,且满足:a2a3=45,a1+a4=14.
(1)求数列{an}的通项公式;
(2)通过公式bn=![]() 构造一个新的数列{bn}.若{bn}也是等差数列,求非零常数c;
构造一个新的数列{bn}.若{bn}也是等差数列,求非零常数c;
(3)对于(2)中得到的数列{bn},求f(n)=![]() (n∈N*)的最大值.
(n∈N*)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点O(0,0),A(1,2),B(4,5)及![]() =
=![]() +t
+t![]() ,
,
求:(1)t为何值时,点P在x轴上?在y轴上?在第二象限?
(2)四边形OABP能否成为平行四边形?若能,求出相应的t值?若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :关于
:关于![]() 的不等式
的不等式![]() 无解;命题
无解;命题![]() :指数函数
:指数函数![]() 是增函数.
是增函数.
(1)若命题![]() 为真命题,求
为真命题,求![]() 的取值范围;
的取值范围;
(2)若满足![]() 为假命题
为假命题![]() 为真命题的实数
为真命题的实数![]() 取值范围是集合
取值范围是集合![]() ,集合
,集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的10000件产品的质量评分服从正态分布![]() . 现从中随机抽取了50件产品的评分情况,结果这50件产品的评分全部介于80分到140分之间.现将结果按如下方式分为6组,第一组
. 现从中随机抽取了50件产品的评分情况,结果这50件产品的评分全部介于80分到140分之间.现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,
, ![]() ,第六组
,第六组![]() ,得到如下图所示的频率分布直方图.
,得到如下图所示的频率分布直方图.

(1)试用样本估计该工厂产品评分的平均分(同一组中的数据用该区间的中间值作代表);
(2)这50件产品中评分在120分(含120分)以上的产品中任意抽取3件,该3件在全部产品中评分为前13名的件数记为![]() ,求
,求![]() 的分布列.
的分布列.
附:若![]() ,则
,则![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:
①数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …的一个通项公式是
…的一个通项公式是![]() ;
;
②当![]() 时,不等式
时,不等式![]() 对一切实数x都成立;
对一切实数x都成立;
③函数![]() 是周期为
是周期为![]() 的奇函数;
的奇函数;
④两两相交且不过同一点的三条直线必在同一个平面内.
其中,正确说法序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学学习习惯不好,把黑板上老师写的表达式忘了,记不清楚是![]() 还是
还是![]() .翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
.翻出草稿本发现在用五点作图法列表作图时曾算出过一些数据(如下表).
| 0 |
|
|
| |
|
|
|
|
| |
| 0 | 3 | 0 | 0 |
(1)请你帮助该同学补充完表格中的数据,写出该函数的表达式![]() ,并写出该函数的最小正周期;
,并写出该函数的最小正周期;
(2)若利用![]() 的图象用图象变化法作
的图象用图象变化法作![]() 的图象,其步骤如下:(在空格内填上合适的变换方法)
的图象,其步骤如下:(在空格内填上合适的变换方法)
第一步:![]() 的图象向右平移
的图象向右平移![]() _____得到
_____得到![]() _____的图象;
_____的图象;
第二步:![]() 的图象(纵坐标不变)______得到
的图象(纵坐标不变)______得到![]() _____的图象;
_____的图象;
第三步:![]() 的图象(横坐标不变)_____得到
的图象(横坐标不变)_____得到![]() 的图象.
的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·开封二模)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率.
(2)检验结束后,甲、乙两名运动员的成绩用茎叶图表示如图:

计算说明哪位运动员的成绩更稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com