
【题目】在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3. 将△BCD沿BD折到△BED的位置,使得二面角E﹣BD﹣A的大小为90°(如图).已知Q为EO的中点,点P在线段AB上,且 ![]() .
.
(Ⅰ)证明:直线PQ∥平面ADE;
(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.
【答案】证明:(Ⅰ)如图,取OD的中点R,连接PR,QR,则DE∥RQ, 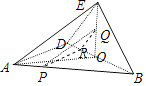
由题知 ![]() ,又
,又 ![]() ,故AB:AP=4:1=DB:DR,因此AD∥PR,
,故AB:AP=4:1=DB:DR,因此AD∥PR,
因为PR,RQ平面ADE,
且AD,DE平面ADE,故PR∥平面ADE,RQ∥平面ADE,
又PR∩RQ=R,
故平面PQR∥平面ADE,从而PQ∥平面ADE.
(Ⅱ)解:由题EA=ED=5, ![]() ,设点O到平面ADE的距离为d,
,设点O到平面ADE的距离为d,
则由等体积法可得 ![]() ,
,
故 ![]() ,因此
,因此 ![]() .
.
【解析】(Ⅰ)证明PR∥平面ADE,RQ∥平面ADE,可得平面PQR∥平面ADE,即可证明:直线PQ∥平面ADE;(Ⅱ)由等体积法可得点O到平面ADE的距离,即可求直线BD与平面ADE所成角θ的正弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
【题目】以下茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.

(1)如果![]() ,求乙组同学单位时间内引体向上次数的平均数和方差;
,求乙组同学单位时间内引体向上次数的平均数和方差;
(2)如果![]() ,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数).
的平均数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3. 将△BCD沿BD折到△BED的位置,使得二面角E﹣BD﹣A的大小为90°(如图).已知Q为EO的中点,点P在线段AB上,且 ![]() .
.
(Ⅰ)证明:直线PQ∥平面ADE;
(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C的参数方程为 ![]() (θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(θ为参数),以O为极点,x轴的非负半轴为极轴且取相同的单位长度建立极坐标系.
(1)求圆C的极坐标方程;
(2)若直线l的极坐标方程是 ![]() ,射线
,射线 ![]() 与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q.求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.?x,y∈R,若x+y≠0,则x≠1且y≠﹣1
B.a∈R,“ ![]() ”是“a>1”的必要不充分条件
”是“a>1”的必要不充分条件
C.命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0”
D.设随机变量X~N(1,52),若P(X<0)=P(X>a﹣2),则实数a的值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小、材质都相同的![]() 个红球,
个红球,![]() 个黑球和
个黑球和![]() 个白球,从口袋中一次摸出一个球,连续摸球两次.
个白球,从口袋中一次摸出一个球,连续摸球两次.
(![]() )如果摸出后不放回,求第一次摸出黑球,第二次摸出白球的概率;
)如果摸出后不放回,求第一次摸出黑球,第二次摸出白球的概率;
(![]() )如果摸出后放回,求恰有一次摸到黑球的概率.
)如果摸出后放回,求恰有一次摸到黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
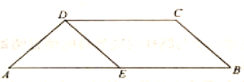
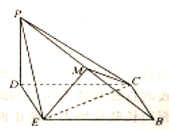
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com