
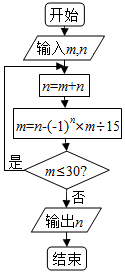
 执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )
执行如图所示的程序框图,如果输入的m,n分别是(2x-y)5的展开式中y2x3,x2y3的系数,则输出的n=( )| A. | 50 | B. | 35 | C. | 20 | D. | 15 |
分析 先求得二项展开式的通项公式,由已知分别令r等于3,2,即可求得m,n的值,然后模拟执行程序,依次写出每次循环得到的m,n的值,当m=35时不满足条件m≤30,退出循环,输出n的值为50.
解答 解:由题意可得:Tr+1=${C}_{5}^{r}$(2x)5-r(-y)r,
令r=3,可得:x2y3的系数即n的值为:${C}_{5}^{3}$×22×(-1)3=-40.
令r=2,可得:x3y2的系数即m的值为:${C}_{5}^{2}$×23×(-1)2=80.
模拟执行程序,可得:
m=80,n=-40,
执行循环体,n=40,m=-25
满足条件m≤30,执行循环体,可得:n=15,m=5
满足条件m≤30,执行循环体,可得:n=20,m=30
满足条件m≤30,执行循环体,可得:n=50,m=35
不满足条件m≤30,退出循环,输出n的值为50.
故选:A.
点评 本题考查了二项式定理的应用,程序框图的应用问题,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或-1 | B. | 2或-1 | C. | 2或1 | D. | 1或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com