考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:法一:由AB∥C1D1,AB=C1D1,BE∥D1F,BE=D1F,且平面ABE∥平面C1D1F,∠ABE=∠C1D1F,知△ABE≌△C1D1F,进而AE=C1F,同理AF=C1E,故AEC1F为平行四边形,由此能够证明A、E、C1、F四点共面.
法二:以C为原点,CD为x轴,CB为y轴,CC1为z轴建立空间直角坐标系,则C1(0,0,3),F(1,0,2),A(1,1,0),E(0,1,1),由此能证明A、E、C1、F四点共面.
解答:
证明:(证法一)∵平行六面体ABCD-A
1B
1C
1D
1中,BE=
BB
1,DF=
DD
1,
∴AB∥C
1D
1,AB=C
1D
1,BE∥D
1F,BE=D
1F,且平面ABE∥平面C
1D
1F,
∠ABE=∠C
1D
1F,
∴△ABE≌△C
1D
1F,…(3分)
∴AE=C
1F,
同理AF=C
1E,
故AEC
1F为平行四边形,
∴A、E、C
1、F四点共面.…(6分)
(2)(法二)(1)以C为原点,CD为x轴,CB为y轴,CC
1为z轴建立如图所示的空间直角坐标系,
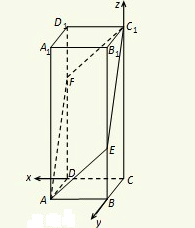
则C
1(0,0,3),F(1,0,2),A(1,1,0),E(0,1,1),…(2分)
∴
=(1,0,-1),
=(1,0,-1),
∴C
1F∥EA,
∴A、E、C
1、F四点共面.…(6分)
点评:本题考查四点共面的证明,解题时要认真审题,注意合理地化空间几何为平面几何进行求解,解题时要注意向量法的合理运用.

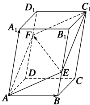 如图所示,在平行六面体ABCD-A1B1C1D1中,EF分别是B1B和D1D上的点,且BE=
如图所示,在平行六面体ABCD-A1B1C1D1中,EF分别是B1B和D1D上的点,且BE=


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案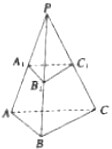 如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证:
如图所示,已知三棱锥P-ABC中,PA=a,PB=b,PC=c,侧棱PA、PB、PC上各有一点A1,B1、C1,且PA1=a1,PB1=b1,PC1=c1,求证: