Question

19．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右两个焦点分别为F₁，F₂，M为圆x²+y²=$\frac{{a}^{2}}{4}$上的点，过左焦点F₁与点M的直线交双曲线右支于点P，若M为线段PF₁的中点，当△PF₁F₂为锐角三角形时，双曲线的离心率范围为$（\sqrt{2}，\frac{\sqrt{10}}{2}）$．

Answer 1

分析 如图所示，M为线段PF₁的中点，O为F₁F₂的中点，可得|PF₂|=2|MO|=a，|PF₁=|PF₂|+2a=3a．当△PF₁F₂为锐角三角形时，∴只有可能∠PF₂F₁或∠F₁PF₂为最大角，因此必然为锐角．利用余弦定理即可得出．

解答 解：如图所示，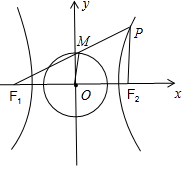
∵M为线段PF₁的中点，O为F₁F₂的中点，
∴|PF₂|=2|MO|=a，|PF₁=|PF₂|+2a=3a．
|F₁F₂|=2c．
∵当△PF₁F₂为锐角三角形时，∴只有可能∠PF₂F₁或∠F₁PF₂为最大角，因此必然为锐角．
∴（2c）²+a²＞（3a）²，且（3a）²+a²＞（2c）²，
可得c²＞2a²，且${c}^{2}＜\frac{5}{2}{a}^{2}$
解得$\sqrt{2}＜e＜\frac{\sqrt{10}}{2}$
故答案为：$（\sqrt{2}，\frac{\sqrt{10}}{2}）$．

点评 本题考查了双曲线的标准方程及其性质、三角形中位线定理、余弦定理，考查了推理能力与计算能力，属于中档题．