
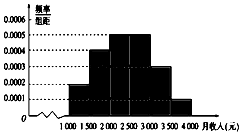
 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).分析 (1)根据频率=小矩形的高×组距来求;
(2)根据中位数的左右两边的矩形的面积和相等,所以只需求出从左开始面积和等于0.5的底边横坐标的值即可,运用取中间数乘频率,再求之和,计算可得平均数,求出众数即可;
(3)求出月收入在[2500,3000)的人数,用分层抽样的抽取比例乘以人数,可得答案.
解答 解:(1)月收入在[3000,3500)的频率为0.0003×500=0.15;
(2)从左数第一组的频率为0.0002×500=0.1;
第二组的频率为0.0004×500=0.2;
第三组的频率为0.0005×500=0.25;
∴中位数位于第三组,设中位数为2000+x,则x×0.0005=0.5-0.1-0.2=0.2⇒x=400.
∴中位数为2400(元)
由1250×0.1+1750×0.2+2250×0.25+2750×0.25+3250×0.15+3750×0.05=2400,
样本数据的平均数为2400(元);
众数是:$\frac{2000+2500}{2}$=2250,和$\frac{2500+3000}{2}$=2750;
(3)月收入在[2500,3000)的频数为0.25×10000=2500(人),
∵抽取的样本容量为100.∴抽取比例为 $\frac{100}{10000}$=$\frac{1}{100}$,
∴月收入在[2500,3000)的这段应抽取2500×$\frac{1}{100}$=25(人).
点评 本题考查了频率分布直方图,分层抽样方法,是统计常规题型,解答此类题的关键是利用频率分布直方图求频数或频率.


科目:高中数学 来源: 题型:选择题
| A. | 3或27 | B. | 3 | C. | 27 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
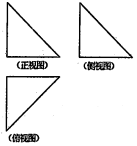 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )
如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )| A. | $\frac{{3+\sqrt{3}}}{2}$ | B. | $3+\sqrt{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com