
| A. | 3或27 | B. | 3 | C. | 27 | D. | 5 |
分析 求出双曲线的a,b,c,设|PF1|=15,运用双曲线的定义,求得|PF2|=3或27,讨论P在左支和右支上,求出最小值,即可判断P的位置,进而得到所求距离.
解答 解:双曲线$\frac{x^2}{36}-\frac{y^2}{64}=1$的a=6,b=8,c=10,
设左右焦点为F1,F2.
则有双曲线的定义,得||PF1|-|PF2||=2a=12,
可设|PF1|=15,则有|PF2|=3或27,
若P在右支上,则有|PF2|≥c-a=4,
若P在左支上,则|PF2|≥c+a=16,
故|PF2|=3舍去;.
故选:C.
点评 本题考查双曲线的方程和定义,考查分类讨论的思想方法,考查运算能力,属于基础题和易错题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | n | 4 | 4.5 |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
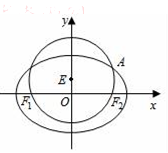 已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.
已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
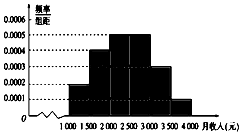 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | $[{kπ,kπ+\frac{π}{2}}]({k∈Z})$ | C. | $[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}]({k∈Z})$ | D. | $[{kπ-\frac{π}{2},kπ}]({k∈Z})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com