练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（　　）
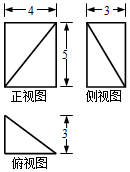
    A．10cm3B．20cm3C．30cm3D．40cm3

    分析 由已知中的三视图可得：该几何体是一个以俯视图为底面的三棱锥切去一个同底同高的三棱锥所得的组合体，进而得到答案．

    解答 解：由已知中的三视图可得：
    该几何体是一个以俯视图为底面的三棱锥切去一个同底同高的三棱锥所得的组合体，
    故体积V=（1-$\frac{1}{3}$）×$\frac{1}{2}$×4×3×5=20cm3，
    故选：B

    点评 本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．若0＜x＜1，则$\frac{1}{x}+\frac{2x}{1-x}$的最小值为（　　）
    A．$2\sqrt{2}$B．1+$2\sqrt{2}$C．2+$2\sqrt{2}$D．3+$2\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知过点A（-2，m）和B（m，4）的直线与直线2x+y-1=0平行，则m的值为-8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知集合P={x|1＜3x≤9}，Q={x∈Z|y=ln（-2x2+7x）}，则P∩Q=（　　）
    A．{1}B．{1，2}C．{2，3}D．{1，2，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数$f（x）=\frac{1}{2}-{cos^2}x+\sqrt{3}sinxcosx$．
    （1）求f（x）单调递增区间；
    （2）△ABC中，角A，B，C的对边a，b，c满足${b^2}+{c^2}-{a^2}＞\sqrt{3}bc$，求f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

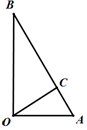    13．根据平面向量基本定理，若$\overrightarrow{e_1}，\overrightarrow{e_2}$为一组基底，同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$，则向量$\overrightarrow a$与有序实数对（x，y）一一对应，称（x，y）为向量$\overrightarrow a$在基底$\overrightarrow{e_1}，\overrightarrow{e_2}$下的坐标；特别地，若$\overrightarrow{e_1}，\overrightarrow{e_2}$分别为x，y轴正方向的单位向量$\overrightarrow i，\overrightarrow j$，则称（x，y）为向量$\overrightarrow a$的直角坐标．
    （I）据此证明向量加法的直角坐标公式：若$\overrightarrow a=（{x_1}，{y_1}），\overrightarrow b=（{x_2}，{y_2}）$，则$\overrightarrow a+\overrightarrow b=（{x_1}+{x_2}，{y_1}+{y_2}）$；
    （II）如图，直角△OAB中，$∠AOB={90°}，|\overrightarrow{OA}|=1，|\overrightarrow{OB}|=\sqrt{3}$，C点在AB上，且$\overrightarrow{OC}⊥\overrightarrow{AB}$，求向量$\overrightarrow{OC}$在基底$\overrightarrow{OA}，\overrightarrow{OB}$下的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知双曲线$\frac{x^2}{36}-\frac{y^2}{64}=1$上一点P到双曲线的一个焦点距离为15，则点P到另外一个焦点的距离为（　　）
    A．3或27B．3C．27D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A，“第2次拿出的是白球”为事件B，则P（B|A）是$\frac{4}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知△ABC中，C=90°，AB=2AC，在斜边AB上任取一点P，则满足∠ACP≤30°的概率为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{5}$

    查看答案和解析>>

    同步练习册答案