
分析 (1)f(x)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化简为一个角的正弦函数,利用正弦函数的增减性确定出f(x)的单调增区间即可;
(2)利用余弦定理表示cosA,整理后代入已知不等式求出cosA的范围,进而求出A的范围,即可确定出f(A)的范围.
解答 解:(1)f(x)=$\frac{1}{2}$-$\frac{1+cos2x}{2}$+$\frac{\sqrt{3}}{2}$sin2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x=sin(2x-$\frac{π}{6}$),
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,得到-$\frac{π}{6}$+kπ≤x≤$\frac{π}{3}$+kπ,k∈Z,
则f(x)的增区间为[-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z);
(2)由余弦定理得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,即b2+c2-a2=2bccosA,
代入已知不等式得:2bccosA>$\sqrt{3}$bc,即cosA>$\frac{\sqrt{3}}{2}$,
∵A为△ABC内角,
∴0<A<$\frac{π}{6}$,
∵f(A)=sin(2A-$\frac{π}{6}$),且-$\frac{π}{6}$<2A-$\frac{π}{6}$<$\frac{π}{6}$,
∴-$\frac{1}{2}$<f(A)<$\frac{1}{2}$,
则f(A)的范围为(-$\frac{1}{2}$,$\frac{1}{2}$).
点评 此题考查了余弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,正弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{5}{2}$ | C. | 2 | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | n | 4 | 4.5 |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
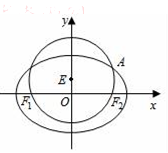 已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.
已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com