
 ����ƽ������������������$\overrightarrow{e_1}��\overrightarrow{e_2}$Ϊһ����ף�ͬһƽ�������$\overrightarrow a$���Ա�Ψһȷ���ر�ʾΪ$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$��������$\overrightarrow a$������ʵ���ԣ�x��y��һһ��Ӧ���ƣ�x��y��Ϊ����$\overrightarrow a$�ڻ���$\overrightarrow{e_1}��\overrightarrow{e_2}$�µ����ꣻ�ر�أ���$\overrightarrow{e_1}��\overrightarrow{e_2}$�ֱ�Ϊx��y��������ĵ�λ����$\overrightarrow i��\overrightarrow j$����ƣ�x��y��Ϊ����$\overrightarrow a$��ֱ�����꣮
����ƽ������������������$\overrightarrow{e_1}��\overrightarrow{e_2}$Ϊһ����ף�ͬһƽ�������$\overrightarrow a$���Ա�Ψһȷ���ر�ʾΪ$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$��������$\overrightarrow a$������ʵ���ԣ�x��y��һһ��Ӧ���ƣ�x��y��Ϊ����$\overrightarrow a$�ڻ���$\overrightarrow{e_1}��\overrightarrow{e_2}$�µ����ꣻ�ر�أ���$\overrightarrow{e_1}��\overrightarrow{e_2}$�ֱ�Ϊx��y��������ĵ�λ����$\overrightarrow i��\overrightarrow j$����ƣ�x��y��Ϊ����$\overrightarrow a$��ֱ�����꣮���� �� I������ƽ���������������㼴��֤�����۳�����
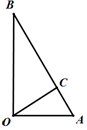
�� II�����ⷨһ�����������������ݼ������ʵó�$\overrightarrow{AC}=\frac{1}{3}\overrightarrow{CB}$����$\overrightarrow{OA}$��$\overrightarrow{OB}$��ʾ$\overrightarrow{OC}$���ɣ�
���ⷨ�����������������ݼ������ʵó�$\overrightarrow{AC}=\frac{1}{4}\overrightarrow{AB}$������$\overrightarrow{OA}$��$\overrightarrow{OB}$��ʾ$\overrightarrow{OC}$���ɣ�
���ⷨ���������귨����OΪ����ԭ�㣬$\overrightarrow{OA}��\overrightarrow{OB}$����Ϊx��y����������ֱ������ϵ��
���������ʾ���$\overrightarrow{OC}$�����꼴�ɣ�
��� �⣺�� I��֤�����������⣺$\overrightarrow a=��{x_1}��{y_1}����\overrightarrow b=��{x_2}��{y_2}��$��
��$\overrightarrow{a}$=x1$\overrightarrow{i}$+y1$\overrightarrow{j}$��$\overrightarrow{b}$=x2$\overrightarrow{i}$+y2$\overrightarrow{j}$����2�֣�
��$\overrightarrow a+\overrightarrow b=��{x_1}+{x_2}��\overrightarrow i+��{y_1}+{y_2}��\overrightarrow j$����4�֣�
��$\overrightarrow a+\overrightarrow b=��{x_1}+{x_2}��{y_1}+{y_2}��$����6�֣�
�� II�����ⷨһ�����������������ݼ������ʣ���֪
��OAB=60�㣬��|$\overrightarrow{CA}$|=$\frac{1}{2}$��|$\overrightarrow{CB}$|=$\frac{3}{2}$��
�Ӷ�$\overrightarrow{AC}=\frac{1}{3}\overrightarrow{CB}$��
��$\overrightarrow{AO}$+$\overrightarrow{OC}$=$\frac{1}{3}$��$\overrightarrow{CO}$+$\overrightarrow{OB}$����
��$\frac{4}{3}$$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$��
����ã�$\overrightarrow{OC}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$��
��$\overrightarrow{OC}$�ڻ���$\overrightarrow{OA}��\overrightarrow{OB}$�µ�����Ϊ$��\frac{3}{4}��\frac{1}{4}��$��
���ⷨ����������������ͬ�Ͽɵã�$\overrightarrow{AC}=\frac{1}{4}\overrightarrow{AB}$��
��$\overrightarrow{AO}$+$\overrightarrow{OC}$=$\frac{1}{4}$��$\overrightarrow{AO}$+$\overrightarrow{OB}$����
��$\overrightarrow{OC}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$���Ӷ���������ʾ��
���ⷨ���������귨������OΪ����ԭ�㣬$\overrightarrow{OA}��\overrightarrow{OB}$����Ϊx��y����������ֱ������ϵ��
��$A��1��0����B��0��\sqrt{3}��$���ɼ���������C��ֱ������Ϊ$��\frac{3}{4}��\frac{{\sqrt{3}}}{4}��$��
��$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$����
$��\frac{3}{4}��\frac{{\sqrt{3}}}{4}��=x��1��0��+y��0��\sqrt{3}��=��x��\sqrt{3}y��$��
��$\left\{\begin{array}{l}{\frac{3}{4}=x}\\{\frac{\sqrt{3}}{4}=\sqrt{3}y}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=\frac{3}{4}}\\{y=\frac{1}{4}}\end{array}\right.$��
��������Ϊ��$\frac{3}{4}$��$\frac{1}{4}$������12�֣�
���� ���⿼����ƽ�����������������������ʾ��Ӧ�����⣬���ۺ�����Ŀ��


 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
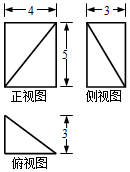
| A�� | 10cm3 | B�� | 20cm3 | C�� | 30cm3 | D�� | 40cm3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com