
分析 (1)若p∧q为真命题,则命题p,q均为真命题,进而可得a的取值范围.
(2)根据命题p、q、r恰有两个是真命题,可得满足条件的实数a的取值范围.
解答 解:(1)若命题p为真命题,则$a<x-\frac{8}{x}$对任意实数x∈[2,4]恒成立
∴$a<{({x-\frac{8}{x}})_{min}}=-2$,即a<-2.…(3分)
若命题q为真命题,则$\frac{4}{a-1}≤{({sinθ-2})_{max}}=-1$,
∴$\frac{4}{a-1}≤-1?\frac{a+3}{a-1}≤0?-3≤a<1$
又∵p∧q为真命题,
∴命题p,q均为真命题,
∴-3≤a<-2…..(6分)
即a的取值范围为[-3,-2)…(7分)
(2)若不等式ax2+2x-1>0有解,则
当a>0时,显然有解;当a=0时,ax2+2x-1>0有解;
当a<0时,∵ax2+2x-1>0有解,∴△=4+4a>0,∴-1<a<0,
∴不等式ax2+2x-1>0有解等价于a>-1,…(10分)
∴若命题p、q、r恰有两个是真命题,
则必有-3≤a<-2或-1<a<1
即a的取值范围为[-3,-2)∪(-1,1).…(12分)
点评 本题以命题的真假判断与应用为载体,考查了复合命题,不等式恒成立问题,存在性问题,二次函数的图象和性质,难度中档.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
 根据平面向量基本定理,若$\overrightarrow{e_1},\overrightarrow{e_2}$为一组基底,同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则向量$\overrightarrow a$与有序实数对(x,y)一一对应,称(x,y)为向量$\overrightarrow a$在基底$\overrightarrow{e_1},\overrightarrow{e_2}$下的坐标;特别地,若$\overrightarrow{e_1},\overrightarrow{e_2}$分别为x,y轴正方向的单位向量$\overrightarrow i,\overrightarrow j$,则称(x,y)为向量$\overrightarrow a$的直角坐标.
根据平面向量基本定理,若$\overrightarrow{e_1},\overrightarrow{e_2}$为一组基底,同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则向量$\overrightarrow a$与有序实数对(x,y)一一对应,称(x,y)为向量$\overrightarrow a$在基底$\overrightarrow{e_1},\overrightarrow{e_2}$下的坐标;特别地,若$\overrightarrow{e_1},\overrightarrow{e_2}$分别为x,y轴正方向的单位向量$\overrightarrow i,\overrightarrow j$,则称(x,y)为向量$\overrightarrow a$的直角坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
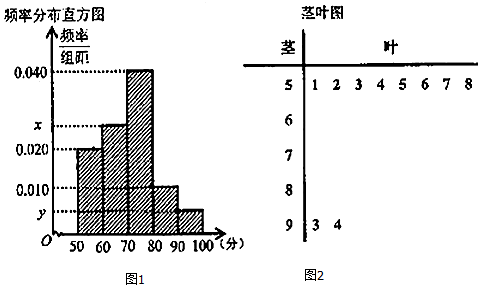
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | $\frac{10}{3}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com