
分析 (1)设单调递增的等差数列{an}的公差为d(d>0),运用等差数列的通项公式和求和公式,得到首项和公差的方程,解方程即可得到所求;
(2)求得${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$=$\frac{2}{(n+1)(n+2)}$=2($\frac{1}{n+1}$-$\frac{1}{n+2}$),运用数列的求和方法:裂项相消求和,可得前n项和为Tn,再解不等式,可得n的最大值.
解答 解:(1)设单调递增的等差数列{an}的公差为d(d>0),
a3,a7,a15成等比数列,可得a72=a3a15,
即(a1+6d)2=(a1+2d)(a1+14d),
化为a1=2d,
又前5项之和等于20,
即有5a1+$\frac{5×4}{2}$d=20,即为a1+2d=4,
解得a1=2,d=1,
数列{an}的通项公式为an=a1+(n-1)d=2+n-1=n+1;
(2)${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$=$\frac{2}{(n+1)(n+2)}$=2($\frac{1}{n+1}$-$\frac{1}{n+2}$),
数列{bn}的前n项和为Tn=2($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=2($\frac{1}{2}$-$\frac{1}{n+2}$)=1-$\frac{2}{n+2}$,
由Tn=1-$\frac{2}{n+2}$,使${T_n}≤\frac{24}{25}$成立,即1-$\frac{2}{n+2}$≤$\frac{24}{25}$,
可得n≤48.
使${T_n}≤\frac{24}{25}$成立的n的最大值为48.
点评 本题考查等差数列的通项公式及求和公式和等比数列中项的性质,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
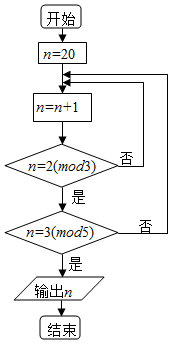 中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )
中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{29}$尺 | B. | $\frac{16}{29}$尺 | C. | $\frac{32}{29}$尺 | D. | $\frac{1}{2}$尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
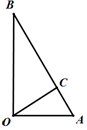 根据平面向量基本定理,若$\overrightarrow{e_1},\overrightarrow{e_2}$为一组基底,同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则向量$\overrightarrow a$与有序实数对(x,y)一一对应,称(x,y)为向量$\overrightarrow a$在基底$\overrightarrow{e_1},\overrightarrow{e_2}$下的坐标;特别地,若$\overrightarrow{e_1},\overrightarrow{e_2}$分别为x,y轴正方向的单位向量$\overrightarrow i,\overrightarrow j$,则称(x,y)为向量$\overrightarrow a$的直角坐标.
根据平面向量基本定理,若$\overrightarrow{e_1},\overrightarrow{e_2}$为一组基底,同一平面的向量$\overrightarrow a$可以被唯一确定地表示为$\overrightarrow a=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则向量$\overrightarrow a$与有序实数对(x,y)一一对应,称(x,y)为向量$\overrightarrow a$在基底$\overrightarrow{e_1},\overrightarrow{e_2}$下的坐标;特别地,若$\overrightarrow{e_1},\overrightarrow{e_2}$分别为x,y轴正方向的单位向量$\overrightarrow i,\overrightarrow j$,则称(x,y)为向量$\overrightarrow a$的直角坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com