
分析 (1)根据平面向量的数量积公式,求出向量的夹角θ的大小;
(2)根据两向量垂直,数量积为0,列出方程求m的值.
解答 解:(1)∵${(\overrightarrow x-2\overrightarrow y)_{\;}}{•_{\;}}(2\overrightarrow x-\overrightarrow y)=5$,
∴2${|\overrightarrow{x}|}^{2}$-5$\overrightarrow{x}$•$\overrightarrow{y}$+2${|\overrightarrow{y}|}^{2}$=5,
又$|{\overrightarrow x}$|=1,$|{\overrightarrow y}$|=2,
∴解得$\overrightarrow{x}$•$\overrightarrow{y}$=1;…(2分)
又∵$cosθ=\frac{{{{\overrightarrow x}_{\;}}{•_{\;}}\overrightarrow y}}{{|{\overrightarrow x}|•|{\overrightarrow y}|}}=\frac{1}{2}$,…(3分)
且θ∈[0,π],
∴$θ=\frac{π}{3}$;…(4分)
(2)∵$(\overrightarrow x-m\overrightarrow y)⊥\overrightarrow y$,
∴${(\overrightarrow x-m\overrightarrow y)_{\;}}{•_{\;}}\overrightarrow y=0$,
即${\overrightarrow x_{\;}}{•_{\;}}\overrightarrow y-m{|{\overrightarrow y}|^2}=0$,…(6分)
∴1-4m=0,
解得m=$\frac{1}{4}$.…(8分)
点评 本题考查了平面向量的数量积与模长公式、垂直的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 6,11,16,21,26 | B. | 3,13,23,33,43 | C. | 5,15,25,36,47 | D. | 10,20,29,39,49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
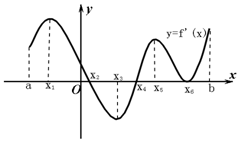 如图是导函数y=f′(x)的图象,对于函数y=f(x)的极值点的说法:?
如图是导函数y=f′(x)的图象,对于函数y=f(x)的极值点的说法:?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com