
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
分析 根据题意,先判定x≥0时f(x)≥1,x<0时f(x)<1,结合条件代入解析式列出两个式子,利用平方关系化简后,由两角差的余弦函数求出cos(α-β)、cos(β-r)的值,可得答案.
解答 解:由题意知,$f(x)=\left\{\begin{array}{l}{{x}^{2}+x+1,x≥0}\\{2x+1,x<0}\end{array}\right.$,
∴x≥0时,x2+x+1≥1,x<0时,2x+1<1;
∵f(sinα+sinβ+sinr-1)=-1,f(cosα+cosβ+cosr+1)=3,
∴2(sinα+sinβ+sinr-1)+1=-1,即sinα+sinβ=-sinr; ①
(cosα+cosβ+sinr+1)2+(cosα+cosβ+cosr+1)+1=3,
得cosα+cosβ+cosr+1=1,即cosα+cosβ=-cosr; ②
①2+②2得,2+2sinαsinβ+2cosαcosβ=1,
∴cosαcosβ+sinαsinβ=$-\frac{1}{2}$,即cos(α-β)=$-\frac{1}{2}$,
同理可求得,cos(β-r)=$-\frac{1}{2}$,
∴cos(α-β)+cos(β-r)=-1,
故选:C.
点评 本题考查了分段函数的应用,两角差的余弦函数,以及平方关系的应用,考查化简、变形能力.


科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
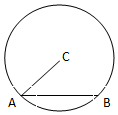
| A. | 8 | B. | -8 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{29}$尺 | B. | $\frac{16}{29}$尺 | C. | $\frac{32}{29}$尺 | D. | $\frac{1}{2}$尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com