
���� ��1������Բ�������̿ɵã�$\frac{\sqrt{6}}{2}$=acos$\frac{��}{6}$��$\frac{1}{2}$=bsin$\frac{��}{6}$�����a��b���ɵ�����C�IJ������̣���Ϊֱ�����귽�̣������ɻ�Ϊ�����귽�̣�
��2������֪�ɵ�ֱ��l�IJ������̣���������C�ķ��̣����ø���ϵ���Ĺ�ϵ�ɵã�|PA|+|PB|��ֵ��
��� �⣺��1��������C�IJ������̣�$\left\{\begin{array}{l}{x=acos��}\\{y=bsin��}\end{array}\right.$����Ϊ��������
�ɵã�$\frac{\sqrt{6}}{2}$=acos$\frac{��}{6}$��$\frac{1}{2}$=bsin$\frac{��}{6}$��
���a=$\sqrt{2}$��b=1��
������C�IJ�������Ϊ$\left\{\begin{array}{l}x=\sqrt{2}cos��\\ y=sin��\end{array}\right.$����ֱ�����귽��Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}=1$��
�伫���귽��Ϊ����2cos2��+2��2sin2��=2��
��2����ֱ��l��P��0��2����б��Ϊ$\sqrt{3}$��
��ֱ��l�IJ�������Ϊ��$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=2+\frac{\sqrt{3}}{2}t\end{array}\right.$��tΪ��������
��������C�ķ��̿ɵã�$\frac{7}{8}$t2+��2$\sqrt{3}+\frac{1}{2}$��t+$\frac{7}{2}$=0��
��|PA|+|PB|=|t1+t2|=$\frac{16\sqrt{3}+4}{7}$
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡���Բ�IJ���ֱ�Ƿ��̼����귽�̵Ļ�������Ӧ�á�ֱ�ߵIJ������̵�Ӧ�ã�������������������������������е���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6��11��16��21��26 | B�� | 3��13��23��33��43 | C�� | 5��15��25��36��47 | D�� | 10��20��29��39��49 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
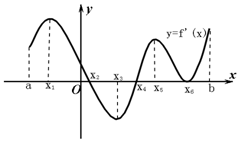 ��ͼ�ǵ�����y=f�䣨x����ͼ���ں���y=f��x���ļ�ֵ���˵����?
��ͼ�ǵ�����y=f�䣨x����ͼ���ں���y=f��x���ļ�ֵ���˵����?�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com