练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
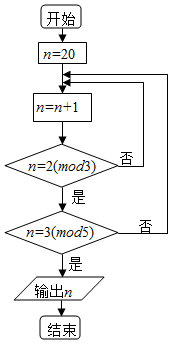
    17．中国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之余二，五五数之余三，问物几何？”人们把此类题目称为“中国剩余定理”，若正整数N除以正整数m后的余数为n，则记为N=n（modm），例如11=2（mod3）．现将该问题以程序框图的算法给出，执行该程序框图，则输出的n等于（　　）
    A．21B．22C．23D．24

    分析 该程序框图的作用是求被3和5除后的余数为2的数，根据所给的选项，得出结论．

    解答 解：该程序框图的作用是求被3除后的余数为2，被5除后的余数为3的数，
    在所给的选项中，满足被3除后的余数为2，被5除后的余数为3的数只有23，
    故选：C．

    点评 本题主要考查程序框图的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的焦距为$2\sqrt{5}$，且双曲线的一条渐近线方程为x-2y=0，则双曲线的方程为（　　）
    A．$\frac{x^2}{4}-{y^2}=1$B．$\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1C．$\frac{{3{x^2}}}{20}-\frac{{3{y^2}}}{5}=1$D．$\frac{{3{x^2}}}{5}-\frac{{3{y^2}}}{20}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．如图，在四棱锥P-ABCD中，AD∥BC，AB⊥AD，AB⊥PA，BC=2AB=2AD=4BE，平面PAB⊥平面ABCD．
    （1）求证：直线ED⊥平面PAC；
    （2）若直线PE与平面PAC所成的角的正弦值为$\frac{\sqrt{5}}{5}$，求二面角A-PC-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知△ABC的边长为a，b，c，定义它的等腰判别式为D=max{a-b，b-c，c-a}+min{a-b，b-c，c-a}，则“D=0”是△ABC为等腰三角形的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

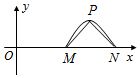    12．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象关于y轴对称，该函数的部分图象如图所示，△PMN是以MN为斜边的等腰直角三角形，且$|MN|•|MP|=2\sqrt{2}$，则f（1）的值为0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．有50件产品，编号从1至50，现从中抽5件检验，用系统抽样的方法确定所抽的编号可能是（　　）
    A．6，11，16，21，26B．3，13，23，33，43C．5，15，25，36，47D．10，20，29，39，49

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．某同学从区间[-1，1]随机抽取2n个数x1，x2，…，xn，y1，y2，…，yn，构成n个数对（x1，y1），（x2，y2），…（xn，yn），该同学用随机模拟的方法估计n个数对中两数的平方和小于1（即落在以原点为圆心，1为半径的圆内）的个数，则满足上述条件的数对约有$\frac{nπ}{4}$个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知△ABC的三个顶点坐标分别为A（1，4）、B（5，-2）、C（1，2），求：
    （1）边BC中点D的坐标；
    （2）BC边上中线AD的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在单调递增的等差数列{an}中，a3，a7，a15成等比数列，前5项之和等于20．
    （1）求数列{an}的通项公式；
    （2）设${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$，记数列{bn}的前n项和为Tn，求使${T_n}≤\frac{24}{25}$成立的n的最大值．

    查看答案和解析>>

    同步练习册答案