
 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.分析 (Ⅰ)由PA⊥平面ABCD,可得AB⊥PA.又AB⊥AD,可建立建立如图所示坐标系.利用向量垂直与数量积的关系、线面垂直的判定定理即可得出.
(Ⅱ)求出平面PAC的一个法向量,设直线PE与平面PAC所成的角为θ,利用向量的数量积解得λ.求出平面PCD的一个法向量利用空间向量的数量积求解即可.
解答 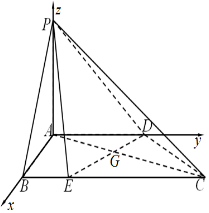 解:(Ⅰ)∵PA⊥平面ABCD,∴AB⊥PA.又∵AB⊥AD,故可建立建立如图所示坐标.
解:(Ⅰ)∵PA⊥平面ABCD,∴AB⊥PA.又∵AB⊥AD,故可建立建立如图所示坐标.
设BC=2AB=2AD=4BE=4,
由已知D(0,2,0),E(2,1,0),C(2,4,0),P(0,0,λ),(λ>0),$\overrightarrow{DE}$=(2,-1,0),
$\overrightarrow{AC}$=(2,4,0),$\overrightarrow{AP}$=(0,0,λ),
$\overrightarrow{DE}$•$\overrightarrow{AC}$=4-4+0=0,$\overrightarrow{DE}$•$\overrightarrow{AP}$=0.
∴DE⊥AC,DE⊥AP,
∴ED⊥平面PAC.
(Ⅱ)由(Ⅰ),平面PAC的一个法向量是$\overrightarrow{DE}$,$\overrightarrow{PE}$=(2,1,λ).
设直线PE与平面PAC所成的角为θ,
∴sinθ=|cos<$\overrightarrow{PE}$,$\overrightarrow{DE}$>|=$\frac{|4-1|}{\sqrt{5}•\sqrt{5+{λ}^{2}}}$=$\frac{\sqrt{5}}{5}$,
解得λ=±2,∵λ>0,∴λ=2,即P(0,0,2).
设平面PCD的一个法向量为$\overrightarrow{n}$=(x,y,z),$\overrightarrow{DC}$=(2,2,0),$\overrightarrow{DP}$=(0,-2,-2),
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DC}=0}\\{\overrightarrow{n}•\overrightarrow{DP}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{2x+2y=0}\\{-2y+2z=0}\end{array}\right.$,取x=1则$\overrightarrow{n}$=(1,-1,-1).
∴cos<$\overrightarrow{n}$,$\overrightarrow{DE}$>=$\frac{2+1}{\sqrt{3}×\sqrt{5}}$=$\frac{\sqrt{15}}{5}$,
显然二面角A-PC-D的平面角是锐角,∴二面角A-PC-D的平面角的余弦值为$\frac{\sqrt{15}}{5}$.
点评 本题考查了空间线面位置关系、法向量的应用、向量垂直与数量积的关系、向量夹角公式,考查了推理能力与计算能力,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{3}-\frac{x^2}{4}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{3}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
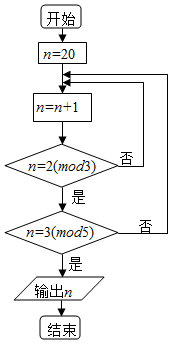 中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )
中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com