
分析 (Ⅰ)先求出平均值$\overline{x}$,再求出标准差.
(Ⅱ)基本事件总数:20,满足条件的基本事件个数:12,由此能求出这两袋的重量都在平均值之下的概率.
解答 解:(Ⅰ)平均值$\overline{x}$=$\frac{1}{9}$(490+495+498+499+500+503+507+506)499.…(3分)
标准差S=$\sqrt{\frac{1}{9}({9}^{2}+{4}^{2}+{6}^{2}+{1}^{2}+{0}^{2}+{1}^{2}+{4}^{2}+{8}^{2}+{7}^{2})}$=$\frac{2\sqrt{66}}{3}$.…(6分)
(Ⅱ)基本事件总数:20,满足条件的基本事件个数:12,
这两袋的重量都在平均值之下的概率:P=$\frac{12}{20}$=$\frac{3}{5}$.…(10分)
点评 本题考查平均值、标准差的求法,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}x±y=0$ | B. | x±y=0 | C. | 2x±y=0 | D. | $\sqrt{3}x±y=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-{y^2}=1$ | B. | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | C. | $\frac{{3{x^2}}}{20}-\frac{{3{y^2}}}{5}=1$ | D. | $\frac{{3{x^2}}}{5}-\frac{{3{y^2}}}{20}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
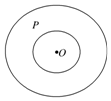 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )| A. | $\frac{1}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com