
分析 (1)根据三角函数的性质可得A,当$x=\frac{π}{12}$时,f(x)取得最大值3;当$x=\frac{7π}{12}$时,f(x)取得最小值-3.求解周期T,可得ω,图象过($\frac{π}{12}$,0),带入求解ϕ,可得f(x)解析式,令ωx+ϕ=kπ,求解对称中心.
(2)将f(x)的解析式带入化简,求解$x∈[{-\frac{π}{3},\frac{π}{6}}]$时,画出f(x)的图象,利用数形结合法,可得实数m的取值范围.
解答 解:(1)由题意可知A=3,
∵在同一周期内,当$x=\frac{π}{12}$时,f(x)取得最大值3;当$x=\frac{7π}{12}$时,f(x)取得最小值-3.
∴$\frac{1}{2}$T=$\frac{7π}{12}-\frac{π}{12}$
∴$T=π=\frac{2π}{ω}$,
∴ω=2.
又∵$2×\frac{π}{12}+ϕ=\frac{π}{2}+2kπ,k∈Z$
得$ϕ=2kπ+\frac{π}{3},k∈Z$,
∵|ϕ|<π,
解得$ϕ=\frac{π}{3}$,
∴函数f(x)的解析式$f(x)=3sin(2x+\frac{π}{3})$.
令$2x+\frac{π}{3}=kπ$得$x=-\frac{π}{6}+\frac{kπ}{2},k∈Z$
∴图象的对称中心为$(-\frac{π}{6}+\frac{kπ}{2},0)$,(k∈Z).
(2)由(1)知$f(x)=3sin(2x+\frac{π}{3})$.
那么:方程2f(x)+1-m=0等价于$sin(2x+\frac{π}{3})=\frac{m-1}{6}$在$x∈[{-\frac{π}{3},\frac{π}{6}}]$上有且仅有一个实数解
∵$x∈[{-\frac{π}{3},\frac{π}{6}}]$,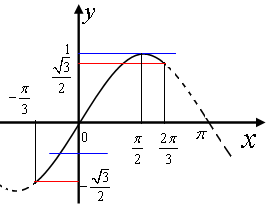
∴$2x+\frac{π}{3}∈[{-\frac{π}{3},\frac{2π}{3}}]$,
令函数y1=sinu,则u∈$[-\frac{π}{3},\frac{2π}{3}]$,其图象为:
结合函数图象有,$\frac{m-1}{6}=1$或$-\frac{{\sqrt{3}}}{2}≤\frac{m-1}{6}<\frac{{\sqrt{3}}}{2}$
解得:m=7或$1-3\sqrt{3}≤m<1+3\sqrt{3}$.
实数m的取值范围为m=7或$1-3\sqrt{3}≤m<1+3\sqrt{3}$.
点评 本题考查正弦函数的图象及性质的运用.采用数形结合法求解参数问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
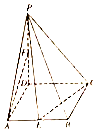 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11,45 | B. | 5,45 | C. | 3,5 | D. | 5,15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com