
分析 (Ⅰ)求出抛物线焦点,直线l方程为y=k(x-1)(k≠0),代入y2=4x利用韦达定理求出x1x2的值即可.
(Ⅱ)通过$\left\{{\begin{array}{l}{y=k(x-n)}\\{{y^2}=4x}\end{array}}\right.$消去x利用韦达定理,通过x1x2+y1y2=0,转化求解n即可.
解答 解:(Ⅰ)由题设知,抛物线焦点F(1,0),…2分
于是直线l方程为y=k(x-1)(k≠0),代入y2=4x得k2x2-2(k2+2)x+k2=0,…4分
显然△=4(k2+2)2-4k4=4(k2+1)>0…5分
由根与系数的关系得${x_1}{x_2}=\frac{k^2}{k^2}=1$.…6分
(Ⅱ)显然k≠0,由$\left\{{\begin{array}{l}{y=k(x-n)}\\{{y^2}=4x}\end{array}}\right.$消去x得${y^2}-\frac{4}{k}y-4n=0$
由题设$△=\frac{16}{k^2}-16n>0$,即1+nk2>0①
由根与系数的关系,得${y_1}+{y_2}=\frac{4}{k}$,y1y2=-4n,②…10分
又x1x2+y1y2=0,${y_1}^2=4{x_1}$,${y_2}^2=4{x_2}$,得y1y2=-16,
由②得n=4,代入①式检验成立,
所以n=4.…12分.
点评 本题考查抛物线的位置关系的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
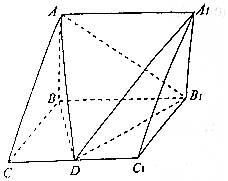 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,∠BCC1=$\frac{π}{3}$,AB=BB1=2,BC=1,D为CC1中点.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,∠BCC1=$\frac{π}{3}$,AB=BB1=2,BC=1,D为CC1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1,2} | B. | {-2,-1,0,1} | C. | {0,1} | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
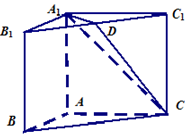 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题:
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.请建立适当的坐标系,求解下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2+ln2] | B. | (1,$\frac{7}{2}$+ln2] | C. | [ln2,2) | D. | (2,$\frac{7}{2}$+ln2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3件都是正品 | B. | 至少有1件次品 | C. | 3件都是次品 | D. | 至少有1件正品 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com