
| A. | (1,2+ln2] | B. | (1,$\frac{7}{2}$+ln2] | C. | [ln2,2) | D. | (2,$\frac{7}{2}$+ln2) |
分析 在同一坐标系中作出函数f(x)和函数g(x)的图象,数形结合可得满足条件的m的取值范围.
解答 解:∵f(x)=e|x|,
∴f(x-2)=e|x-2|,
在同一坐标系中作出函数f(x)和函数g(x)的图象如下图所示: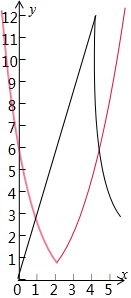
由图可得:当x=1时,f(x-2)=g(x)=e,
当x=4时,f(x-2)=e2<g(x)=4e,
当x>4时,由f(x-2)=ex-2≤g(x)=4e5-x得:e2x-7≤4,
解得:x≤ln2+$\frac{7}{2}$,
对任意的x∈[1,m](m>1),都有f(x-2)≤g(x),
则m∈(1,$\frac{7}{2}$+ln2],
故选:B
点评 本题考查的知识点是指数函数的图象与性质,数形结合思想,难度中档,在同一坐标系中画出两个函数的图象是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | -$\overrightarrow{a}$+3$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-3$\overrightarrow{b}$ | C. | 3$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | -3$\overrightarrow{a}$+$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
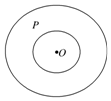 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )| A. | $\frac{1}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow 0$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{BD}$ | D. | $\overrightarrow{DA}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com