练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．在△ABC中，BC=5，CA=8，∠C=60°，则$\overrightarrow{BC}•\overrightarrow{CA}$=-20．

    分析 由题意画出图形，直接代入数量积公式求解．

    解答 解：如图，

    ∵BC=5，CA=8，∠C=60°，
    ∴$\overrightarrow{BC}•\overrightarrow{CA}$=$|\overrightarrow{BC}||\overrightarrow{CA}|cos120°=5×8×（-\frac{1}{2}）=-20$．
    故答案为：-20．

    点评 本题考查平面向量的数量积运算，考查数形结合的解题思想方法，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．二进制数1101100（2）化为十进制数是108．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

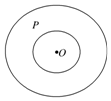    11．如图，“天宫一号”运行的轨迹是如图的两个类同心圆，小圆的半径为2km，大圆的半径为4km，卫星P在圆环内无规则地自由运动，运行过程中，则点P与点O的距离小于3km的概率为（　　）
    A．$\frac{1}{12}$B．$\frac{5}{12}$C．$\frac{1}{3}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．如图，在四棱锥P-ABCD中，AD∥BC，AB⊥AD，AB⊥PA，BC=2AB=2AD=4BE，平面PAB⊥平面ABCD．
    （1）求证：直线ED⊥平面PAC；
    （2）若直线PE与平面PAC所成的角的正弦值为$\frac{\sqrt{5}}{5}$，求二面角A-PC-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．化简 $\overrightarrow{AB}-\overrightarrow{CD}+\overrightarrow{BD}-\overrightarrow{AC}$的结果是（　　）
    A．$\overrightarrow 0$B．$\overrightarrow{AC}$C．$\overrightarrow{BD}$D．$\overrightarrow{DA}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知△ABC的边长为a，b，c，定义它的等腰判别式为D=max{a-b，b-c，c-a}+min{a-b，b-c，c-a}，则“D=0”是△ABC为等腰三角形的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

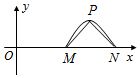    12．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象关于y轴对称，该函数的部分图象如图所示，△PMN是以MN为斜边的等腰直角三角形，且$|MN|•|MP|=2\sqrt{2}$，则f（1）的值为0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．某同学从区间[-1，1]随机抽取2n个数x1，x2，…，xn，y1，y2，…，yn，构成n个数对（x1，y1），（x2，y2），…（xn，yn），该同学用随机模拟的方法估计n个数对中两数的平方和小于1（即落在以原点为圆心，1为半径的圆内）的个数，则满足上述条件的数对约有$\frac{nπ}{4}$个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

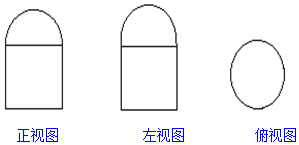    7．如图所示，是一个组合体的三视图，图中四边形是边长为2的正方形，圆的直径为2，那么这个组合体的表面积是（　　）
    A．5πB．6πC．7πD．8π

    查看答案和解析>>

    同步练习册答案