
分析 根据题意,利用条件概率计算公式求出事件A发生的条件下事件B发生的概率即可.
解答 解:一个口袋中装有5个白球,3个红球,每次从袋中随机摸出一个球,不放回地摸2次,
A表示“第一次拿出的是白球”,B表示“第二次拿出的是白球”,
则P(A)=$\frac{5}{8}$,P(AB)=$\frac{5}{8}×\frac{4}{7}$=$\frac{5}{14}$;
在摸出的第一个是白球的条件下,摸出的第二个球是白球的概率是:
p(B|A)=$\frac{\frac{5}{14}}{\frac{5}{8}}$=$\frac{4}{7}$.
故答案为$\frac{4}{7}$.
点评 本题考查了条件概率的计算问题,是基础题目.


科目:高中数学 来源: 题型:选择题
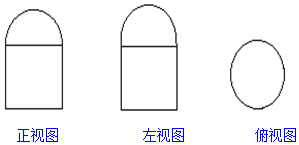 如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )| A. | 5π | B. | 6π | C. | 7π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
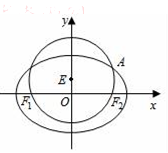 已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.
已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$,经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且与直线OA平行.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
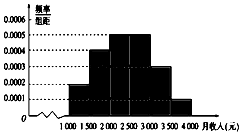 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{11}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com