
| A. | ② | B. | ②③ | C. | ③④ | D. | ①④ |
分析 ①利用线面垂直的性质可得:若m⊥α,n⊥α,则m∥n;
②利用平面平行的传递性和平行平面的性质可得:若α∥β,β∥γ,则α∥γ,又m⊥α,则m⊥γ;
③利用线面平行的性质可得:若m∥α,n∥α,则m∥n、相交或为异面直线;
④利用面面垂直的性质可得:若α⊥γ,β⊥γ,则α∥β或相交.
解答 解:①若m⊥α,n⊥α,则m∥n,因此①不正确;
②若α∥β,β∥γ,则α∥γ,又m⊥α,则m⊥γ,正确;
③若m∥α,n∥α,则m∥n、相交或为异面直线,因此不正确;
④若α⊥γ,β⊥γ,则α∥β或相交,因此不正确.
综上可知:只有②正确.
点评 本题综合考查了空间中线面的位置关系及其判定性质,属于基础题.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
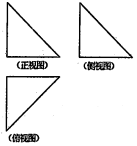 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )
如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )| A. | $\frac{{3+\sqrt{3}}}{2}$ | B. | $3+\sqrt{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 6 | C. | $\frac{10}{3}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,5} | B. | {0,1,2} | C. | {0,1,5} | D. | {0,2,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com