
【题目】已知函数![]()
求证:(1)![]()
(2)对![]() ,若
,若![]() ,
,![]() =1,求证:
=1,求证: ![]()
【答案】(1)见解析;(2)见解析.
【解析】试题分析:
(1)利用函数的单调性结合函数的定义域即可证得结论;
(2)结合题意利用数学归纳法证明结论即可.
试题解析:
⑴x>0时,![]() =x
=x![]()
![]() 0,f(x)单调增,f(x)
0,f(x)单调增,f(x) ![]() f(0)=0
f(0)=0
⑵①![]()
![]()
![]() =
=![]() , x1=1
, x1=1![]()
![]() >1,
>1,![]() >0对任意n成立;
>0对任意n成立;
又⑴知f(![]() )
)![]() 0
0![]()
![]() -1<
-1<![]() ,从而
,从而![]() <
<![]() ,
,![]() ,数列{
,数列{![]() }单调减,
}单调减,
②下面用数学归纳法证明![]()
当n=1时,![]() =1>
=1>![]() ,命题成立
,命题成立
假设n=k时,命题成立,即![]()
要证![]() >
>![]() ,只要证明
,只要证明![]() ,只要证明
,只要证明![]() >
>![]()
设g(x)=![]() ,
,![]() =
=![]() =-
=-![]() >0在x>0上成立,
>0在x>0上成立,
故g(x)在x>0上单调增,![]() ,g(
,g(![]() )=
)=![]() >g(
>g(![]() ),
),
只要证明g(![]() )=
)=![]() >
>![]() =
=![]() ,设
,设![]() ≥
≥![]() =t>0,
=t>0,
只要证明![]() ,只要证明
,只要证明![]() -1>t
-1>t![]()
设![]() -1-t
-1-t![]() =h(t),t>0,
=h(t),t>0,![]() =
=![]() >0在t>0时恒成立,
>0在t>0时恒成立,
h(t)单调增,h(t)>h(0)=0, ![]() -1>t
-1>t![]() 成立。从而对n=k+1,不等式仍然成立
成立。从而对n=k+1,不等式仍然成立
总之,![]() 成立
成立


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC. 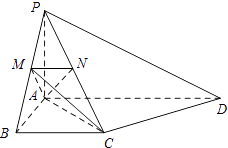
(1)证明:平面AMN⊥平面PBA;
(2)若M为PB的中点,求二面角M﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所设计了一款智能机器人,为了检验设计方案中机器人动作完成情况,现委托某工厂生产![]() 个机器人模型,并对生产的机器人进行编号:
个机器人模型,并对生产的机器人进行编号: ![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的机器人样本,试验小组对
的机器人样本,试验小组对![]() 个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
个机器人样本的动作个数进行分组,频率分布直方图及频率分布表中的部分数据如图所示,请据此回答如下问题:
分组 | 机器人数 | 频率 |
| 0.08 | |
| 10 | |
| 10 | |
| ||
| 6 |

(1)补全频率分布表,画出频率分布直方图;
(2)若随机抽的第一个号码为![]() ,这
,这![]() 个机器人分别放在
个机器人分别放在![]() 三个房间,从
三个房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,从
房间,从![]() 到
到![]() 在
在![]() 房间,求
房间,求![]() 房间被抽中的人数是多少?
房间被抽中的人数是多少?
(3)从动作个数不低于![]() 的机器人中随机选取
的机器人中随机选取![]() 个机器人,该
个机器人,该![]() 个机器人中动作个数不低于
个机器人中动作个数不低于![]() 的机器人记为
的机器人记为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列不等关系正确的是( )
A.( ![]() )
) ![]() <34<(
<34<( ![]() )﹣2
)﹣2
B.( ![]() )﹣2<(
)﹣2<( ![]() )
) ![]() <34
<34
C.(2.5)0<( ![]() )2.5<22.5
)2.5<22.5
D.( ![]() )2.5<(2.5)0<22.5
)2.5<(2.5)0<22.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中,
中, ![]() 是椭圆的左、右焦点,过
是椭圆的左、右焦点,过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,若
两点,若![]() 的周长为8,离心率为
的周长为8,离心率为![]() .
.
(1)求椭圆方程;
(2)若弦![]() 的斜率不为0,且它的中垂线与
的斜率不为0,且它的中垂线与![]() 轴交于
轴交于![]() ,求
,求![]() 的纵坐标的范围;
的纵坐标的范围;
(3)是否在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,且f(﹣2)=3,f(﹣1)=f(1).
,且f(﹣2)=3,f(﹣1)=f(1).
( I)求f(x)的解析式;
( II)画出f(x)的图象(不写过程)并求其值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行抽奖活动,规则如下:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和3个黑球,这些球除颜色外完全相同;每次抽奖都从这两个箱子里各随机地摸出2个球,若摸出的白球个数不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)在一次游戏中,求获奖的概率;
(2)在三次游戏中,记获奖次数为随机变量X,求X的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com