
(本小题满分12分)袋中有大小相同的红、黄两种颜色的球各1个,从中任取1只,有放回地抽取3次.求:
(Ⅰ)3只全是红球的概率;
(Ⅱ)3只颜色全相同的概率;
(Ⅲ)3只颜色不全相同的概率.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ) 。
。
解析试题分析:解法一:由于是有放回地取球,因此袋中每只球每次被取到的概率均为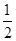 .
.
(Ⅰ)3只全是红球的概率为P1=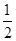 ·
·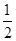 ·
·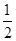 =
= .
.
(Ⅱ)3只颜色全相同的概率为P2=2·P1=2· =
= .
.
(Ⅲ)3只颜色不全相同的概率为P3=1-P2=1- =
= .
.
解法二:利用树状图我们可以列出有放回地抽取3次球的所有可能结果: ,
,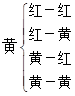 .
.
由此可以看出,抽取的所有可能结果为8种.所以
(Ⅰ)3只全是红球的概率为P1= .
.
(Ⅱ)3只颜色全相同的概率为P2=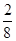 =
= .
.
(Ⅲ)3只颜色不全相同的概率为P3=1-P2=1- =
= .
.
考点:等可能事件的概率;相互独立事件的概率乘法公式;互斥事件与对了事件。
点评:本题主要考查等可能事件的概率,相互独立事件同时发生的概率,本题解题的关键是看清条件中所给的是有放回的抽样,注意区别有放回和无放回两种不同的情况,本题是一个中档题目.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) |  | 30 | 25 |  | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
 的值,并求顾客一次购物的结算时间
的值,并求顾客一次购物的结算时间 的分布列与数学期望;
的分布列与数学期望; 分钟的概率.(注:将频率视为概率)
分钟的概率.(注:将频率视为概率)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)设 为坐标原点,点
为坐标原点,点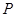 的坐标
的坐标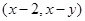
(1)在一个盒子中,放有标号为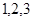 的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为
的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为 ,求|
,求| |的最大值,并求事件“|
|的最大值,并求事件“| |取到最大值”的概率;
|取到最大值”的概率;
(2)若利用计算机随机在[ ,
, ]上先后取两个数分别记为
]上先后取两个数分别记为 ,
,
求: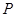 点在第一象限的概率.
点在第一象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某项计算机考试按科目A、科目B依次进行,只有大拿感科目A成绩合格时,才可继续参加科目B的考试,已知每个科目只允许有一次补考机会,两个科目均合格方快获得证书,现某人参加这项考试,科目A每次考试成绩合格的概率为 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为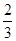 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这次考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为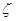 ,求随即变量
,求随即变量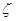 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某机构向民间招募防爆犬,首先进行入围测试,计划考察三个项目:体能,嗅觉和反应.这三个项目中只要有两个通过测试,就可以入围.某训犬基地有4只优质犬参加测试,已知它们通过体能测试的概率都是1/3,通过嗅觉测试的概率都是1/3,通过反应测试的概率都是1/2.
求(1)每只优质犬能够入围的概率;
(2)若每入围1只犬给基地记10分,设基地的得分为随机变量ξ,求ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ,命中得
,命中得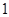 分,没有命中得
分,没有命中得 分;向乙靶射击两次,每次命中的概率为
分;向乙靶射击两次,每次命中的概率为 ,每命中一次得
,每命中一次得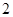 分,没有命中得
分,没有命中得 分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(1)求该射手恰好命中一次的概率;(2)求该射手的总得分
分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(1)求该射手恰好命中一次的概率;(2)求该射手的总得分 的分布列及数学期望
的分布列及数学期望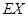 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的以 为圆心的转盘一次,并获得相应金额的返券,假定指针等可能地指向任一位置(不指向各区域的边界). 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
为圆心的转盘一次,并获得相应金额的返券,假定指针等可能地指向任一位置(不指向各区域的边界). 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(Ⅰ)若某位顾客消费128元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为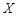 (元).求随机变量
(元).求随机变量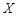 的分布列和数学期望.
的分布列和数学期望. 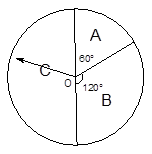
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com