
(本小题满分12分)
某项计算机考试按科目A、科目B依次进行,只有大拿感科目A成绩合格时,才可继续参加科目B的考试,已知每个科目只允许有一次补考机会,两个科目均合格方快获得证书,现某人参加这项考试,科目A每次考试成绩合格的概率为 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为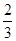 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这次考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为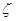 ,求随即变量
,求随即变量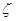 的分布列和数学期望.
的分布列和数学期望.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在
下落的过程中,将3次遇到黑色障碍物,最后落入 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是 .
.
(Ⅰ)求小球落入 袋中的概率
袋中的概率 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记 为落入
为落入 袋中的小球个数,试求
袋中的小球个数,试求 的概率和
的概率和 的数学期望
的数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为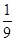 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为 ,试写出
,试写出 的分布列,并求
的分布列,并求 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)文科班某同学参加广东省学业水平测试,物理、化学、生物获得等级A和获得等级不是A的机会相等,物理、化学、生物获得等级A的事件分别记为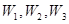 ,物理、化学、生物获得等级不是A的事件分别记为
,物理、化学、生物获得等级不是A的事件分别记为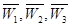 .
.
(I)试列举该同学这次水平测试中物理、化学、生物成绩是否为A的所有可能结果(如三科成绩均为A记为(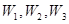 );
);
(II)求该同学参加这次水平测试获得两个A的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)袋中有大小相同的红、黄两种颜色的球各1个,从中任取1只,有放回地抽取3次.求:
(Ⅰ)3只全是红球的概率;
(Ⅱ)3只颜色全相同的概率;
(Ⅲ)3只颜色不全相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| | “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
 ,其中
,其中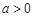 ,
,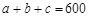 。当数据
。当数据 的方差
的方差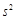 最大时,写出
最大时,写出 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时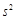 的值.
的值.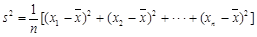 ,其中
,其中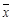 为数据
为数据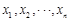 的平均数)
的平均数)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学在高三开设了4门选修课,每个学生必须且只需选修1门选修课。对于该年级的甲、乙、丙3名学生,回答下面的问题:
(1)求这3名学生选择的选修课互不相同的概率;
(2)某一选修课被这3名学生选修的人数的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com