练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．掷一枚均匀的硬币，如果连续抛掷1000次，那么第999次出现正面向上的概率是（　　）
    A．$\frac{1}{1000}$B．$\frac{1}{999}$C．$\frac{1}{2}$D．$\frac{999}{1000}$

    分析 简化模型，只考虑第999次出现的结果，有两种结果，第999次出现正面朝上只有一种结果，即可求出．

    解答 解：抛掷一枚质地均匀的硬币，只考虑第999次，
    有两种结果：正面朝上，反面朝上，每中结果等可能出现，
    故所求概率为$\frac{1}{2}$，
    故选：C．

    点评 本题主要考查了古典概率中的等可能事件的概率的求解，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．下列各选项中的M与P表示同一个集合的是（　　）
    A．M={x∈R|x2+0.01=0}，P={x|x2=0}B．M={（x，y）|y=x2，x∈R}，P={y|y=x2，x∈R}
    C．M={y|y=t2+1，t∈R}，P={t|t=（y-1）2+1，y∈R}D．M={x|x=2k，k∈Z}，P={x|x=4k+2，k∈Z}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．由正整数组成的一组数据x1，x2，x3，x4，其平均数和中位数都是2，且标准差等于1，则这组数据的立方和为（　　）
    A．70B．60C．50D．56

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．△ABC中，∠B=60°，b=2$\sqrt{3}$，则△ABC周长的最大值为（　　）
    A．2B．2$\sqrt{3}$C．3$\sqrt{3}$D．6$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

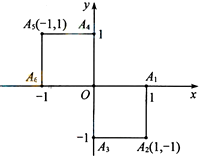    5．小波以游戏的方式决定是去打球、唱歌还是去下棋．游戏规则为以O为起点，再从A1，A2，A3，A4，A5，A6（如图）这6个点中任取两点分别为终点得到两个向量，记住这两个向量的数量积为X，若X＞0就去打球，若X=0就去唱歌，若X＜0就去下棋．
    （1）写出数量积X的所有可能取值
    （2）分别求小波去下棋的概率和不去唱歌的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

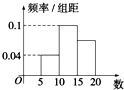    15．如图是一组样本数据的频率分布直方图，则依据图形中的数据，可以估计总体的平均数与中位数分别是（　　）
    A．12.5，12.5B．13.5，13C．13.5，12.5D．13，13

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=Asin（2x+φ），x∈R，A＞0，φ∈（0，$\frac{π}{2}$），且f（$\frac{π}{12}$）=f（$\frac{π}{4}$）=$\sqrt{3}$．
    （Ⅰ）求A，φ的值；
    （Ⅱ）若f（x0）=$\frac{6}{5}$，x0∈[$\frac{π}{4}$，$\frac{π}{2}$]，求sin（2x0-$\frac{π}{12}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若x＞0，y＞0，且x（x+y）=5x+y，则2x+y的最小值为9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．对任意一个非零复数z，定义集合Mz={w|w=zn，n∈N*}．设α是方程x+$\frac{1}{x}$=0的一个根，若在Ma中任取两个数，则其和为零的概率P=$\frac{1}{3}$．

    查看答案和解析>>

    同步练习册答案