
| A.1 | B.2 | C.0 | D.视a的值而定 |
科目:高中数学 来源:不详 题型:解答题
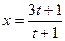 。已知2010年生产饮料的设备折旧
。已知2010年生产饮料的设备折旧 ,维修等固定费用为3 万元,每生产1万件
,维修等固定费用为3 万元,每生产1万件 成本—促销费,生产成本=固定费用+生产费用)
成本—促销费,生产成本=固定费用+生产费用)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
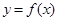 ,有下列五个命题:
,有下列五个命题: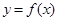 存在反函数,且与反函数图象有公共点,则公共点一定在直线
存在反函数,且与反函数图象有公共点,则公共点一定在直线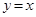 上;
上;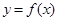 在
在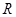 上有定义,则
上有定义,则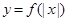 一定是偶函数;
一定是偶函数;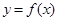 是偶函数,且
是偶函数,且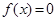 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;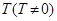 是函数
是函数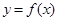 的周期,则
的周期,则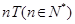 ,也是函数
,也是函数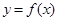 的周期;
的周期;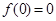 是函数
是函数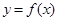 为奇函数的充分不必要条件。
为奇函数的充分不必要条件。A.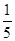 | B.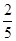 | C.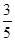 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
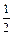 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com