
科目:高中数学 来源:不详 题型:解答题
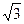 米,记∠BHE=θ.
米,记∠BHE=θ.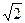 ,求此时管道的长度L;
,求此时管道的长度L;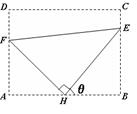
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分) 2010年11月在广州召开亚
分) 2010年11月在广州召开亚 运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平
运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平 均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均
均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均 销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).
销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com