
分析 (1)根据求导公式和法则求出已知函数的导数即可.
(2)根据定积分的计算方法计算即可,
解答 解(1):∵$y=\sqrt{x}-\frac{1}{2}sinx+{e^{-x}}∴y'=\frac{1}{{2\sqrt{x}}}-\frac{1}{2}cosx-{e^{-x}}$
(2):原式=$\int_{-3}^{-2}{({x^2}-4)dx+\int_{-2}^1{(4-{x^2})dx}}$=($\frac{1}{3}$x3-4x)|${\;}_{-3}^{-2}$+(4x-$\frac{1}{3}$x3)|${\;}_{-2}^{1}$=$\frac{34}{3}$.
故答案为:$\frac{34}{3}$.
点评 本题考查了求导公式和法则和定积分的计算,是基础题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
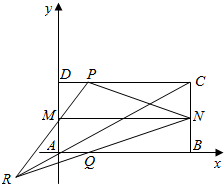 如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),
如图所示,已知四边形ABCD是矩形,M,N分别是AD,BC的中点,P是CD上一点,Q是AB上一点,PM与QN交于R,A是原点,B(2,0),C(2,1),D(0,1),P(t,1),Q(t,0),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a+\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow a-\overrightarrow b$,$\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$,$2\overrightarrow a+\overrightarrow b$ | D. | $2\overrightarrow a-2\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
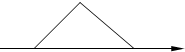 用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )
用斜二测画法得到某三角形的水平放置的直观图是一个等腰直角三角形(如图所示,其中的x轴表示水平方向),斜边长为2,则原三角形的面积为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )
如图,四边形OABC是边长为1的正方形,OD=3,点P为线段CD上的动点,设$\overrightarrow{OP}$=α$\overrightarrow{OB}$+β$\overrightarrow{OD}$,则α+β的取值范围是( )| A. | [$\frac{2}{3}$,2] | B. | [0,$\frac{2}{3}$] | C. | [1,2] | D. | [$\frac{2}{3}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com