
| A. | $\overrightarrow a+\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow a-\overrightarrow b$,$\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$,$2\overrightarrow a+\overrightarrow b$ | D. | $2\overrightarrow a-2\overrightarrow b$,$\overrightarrow a-\overrightarrow b$ |
分析 判断向量是否共线,推出结果即可.
解答 解:$\overrightarrow a-\overrightarrow b$=-($\overrightarrow b-\overrightarrow a$),选项B的两个向量共线,不正确;
$2(\overrightarrow{a}+\frac{1}{2}\overrightarrow{b})=2\overrightarrow{a}+\overrightarrow{b}$,选项C的两个向量共线,不正确;
$2\overrightarrow{a}-2\overrightarrow{b}=2(\overrightarrow{a}-\overrightarrow{b})$,选项D的两个向量共线,不正确;
故选:A.
点评 本题考查平面向量基本定理的应用,基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\frac{1}{2\sqrt{2}}$ | C. | $\frac{1}{2\sqrt{3}}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
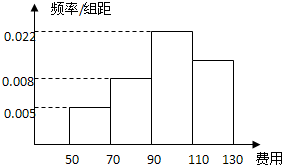 学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )
学校为了解学生每周在校费用情况,抽取了n个同学进行调查,结果显示这些同学的支出都在[50,130](单位:元),其中支出在[50,70)(单位:元)的同学有40人,其频率分布直方图如图所示,则支出在[110,130](单位:元)的同学人数是( )| A. | 100 | B. | 120 | C. | 30 | D. | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com