练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)满足f(－x)＝f(x)，且当x≥0时，f(x)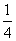＝()x，又函数g(x)＝|xsinπx|，则函数h(x)＝f(x)－g(x)在[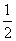－，2]上的零点个数为(　　)

    A．3　　　　B．4　　　　C．5　　　　D．6


    C

    [解析]　

    由题意知f(x)，g(x)均为偶函数，所以函数h(x)在[－，2]上的零点个数可转化为在区间[0，]上的零点个数和在区间(0,2]上的零点个数之和．当x∈(0,2]时，令h(x)＝0，即()x＝|xsinπx|，则|sinπx|＝·()x，画出函数y＝|sinπx|和y＝·()x的图象如图所示，由图可知两图象有4个交点，且x＝是其中一个交点，所以函数h(x)在[－，2]上有5个零点．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     关于综合法和分析法说法错误的是              （    ）

        A. 综合法和分析法是直接证明中最基本的两种证明方法

        B. 综合法又叫顺推证法或由因导果法

        C. 分析法又叫逆推证法或执果索因法

        D. 综合法和分析法都是因果分别互推的两头凑法

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出命题：若函数y＝f(x)是幂函数，则函数y＝f(x)的图象不过第四象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是(　　)

    A．3　　　　B．2　　　　C．1　　　　D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的偶函数y＝f(x)，当x≥0时，y＝f(x)是单调递增的，f(1)·f(2)<0.则函数y＝f(x)的图象与x轴的交点个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若定义在R上的函数y＝f(x)满足f(x＋1)＝－f(x)，且当x∈[－1,1]时，f(x)＝x2，函数g(x)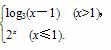＝则函数h(x)＝f(x)－g(x)在区间[－5,5]内的零点的个数为(　　)

    A．9　　　　B．8　　　　C．7　　　　D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a∈{1,2,3,4}，b∈{2,4,8,12}，则函数f(x)＝x3＋ax－b在区间[1,2]上有零点的概率为(　　)

    A.　　　  B.　　　

    C.　 　  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点P(x，y)是直线kx＋y＋4＝0(k＞0)上一动点，PA，PB是圆C：x2＋y2－2y＝0的两条切线，A，B为切点，若四边形PACB的最小面积是2，则k的值为(　　)

    A．4                                                     B．3

    C．2                                                     D.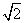

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点M(3,1)，直线ax－y＋4＝0及圆(x－1)2＋(y－2)2＝4.

    (1)求过M点的圆的切线方程；

    (2)若直线ax－y＋4＝0与圆相切，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列中，已知，，则            。

    查看答案和解析>>

    同步练习册答案