
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,若存在两项
,若存在两项![]() ,使得
,使得![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
运用数列的递推式和等比数列的定义、通项公式可得an=2n.求得m+n=6,![]() (m+n)(
(m+n)(![]() )
)![]() (3
(3![]() ),运用基本不等式,检验等号成立的条件,即可得到所求最小值.
),运用基本不等式,检验等号成立的条件,即可得到所求最小值.
Sn=2an﹣2,可得a1=S1=2a1﹣2,即a1=2,
n≥2时,Sn﹣1=2an﹣1﹣2,又Sn=2an﹣2,
相减可得an=Sn﹣Sn﹣1=2an﹣2an﹣1,即an=2an﹣1,
{an}是首项为2,公比为2的等比数列.
所以an=2n.
aman=64,即2m2n=64,
得m+n=6,
所以![]() (m+n)(
(m+n)(![]() )
)![]() (3
(3![]() )
)![]() (3+2
(3+2![]() ),
),
当且仅当![]() 时取等号,即为m
时取等号,即为m![]() ,n
,n![]() .
.
因为m、n取整数,所以均值不等式等号条件取不到,则![]() (3+2
(3+2![]() ),
),
验证可得,当m=2,n=4,或m=3,n=3,,![]() 取得最小值为
取得最小值为![]() .
.
故选:B.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】给定椭圆![]() :
:![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)设椭圆短轴的一个端点为![]() ,长轴的一个端点为
,长轴的一个端点为![]() ,点
,点![]() 是“准圆”上一动点,求三角形
是“准圆”上一动点,求三角形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】再直角坐标系中,定义两点![]() ,
,![]() 间的“直角距离”为
间的“直角距离”为![]() ,现有下列命题:
,现有下列命题:
①若![]() ,
,![]() 是
是![]() 轴上两点,则
轴上两点,则![]()
②已知![]() ,
,![]() ,则
,则![]() 为定值
为定值
③原点![]() 到直线
到直线![]() 上任一点
上任一点![]() 的直角距离
的直角距离![]() 的最小值为
的最小值为![]()
④设![]() 且
且![]() ,
,![]() ,若点
,若点![]() 是在过
是在过![]() 与
与![]() 的直线上,且点
的直线上,且点![]() 到点
到点![]() 与
与![]() 的“直角距离”之和等于
的“直角距离”之和等于![]() ,那么满足条件的点
,那么满足条件的点![]() 只有
只有![]() 个.
个.
其中的真命题是____________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织高一年级学生到古都西安游学.在某景区,由于时间关系,每个班只能在甲、乙、丙三个景点中选择一个游览.高一![]() 班的
班的![]() 名同学决定投票来选定游览的景点,约定每人只能选择一个景点,得票数高于其它景点的入选.据了解,在甲、乙两个景点中有
名同学决定投票来选定游览的景点,约定每人只能选择一个景点,得票数高于其它景点的入选.据了解,在甲、乙两个景点中有![]() 人会选择甲,在乙、丙两个景点中有
人会选择甲,在乙、丙两个景点中有![]() 人会选择乙.那么关于这轮投票结果,下列说法正确的是
人会选择乙.那么关于这轮投票结果,下列说法正确的是
①该班选择去甲景点游览;
②乙景点的得票数可能会超过![]() ;
;
③丙景点的得票数不会比甲景点高;
④三个景点的得票数可能会相等.
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
①![]() 在
在![]() 上是减函数;
上是减函数;
②![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
③![]() 在
在![]() 上至少有两个零点.
上至少有两个零点.
其中正确结论的序号为_________(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设D,E分别为PA,AC中点.
.设D,E分别为PA,AC中点.
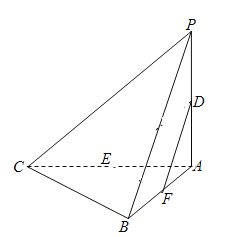
(Ⅰ)求证:![]() 平面PBC;
平面PBC;
(Ⅱ)求证:![]() 平面PAB;
平面PAB;
(Ⅲ)试问在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC平行?若存在,指出点F的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问5分,(2)小问7分)
如图,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 过
过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]()

(1)若![]() ,求椭圆的标准方程
,求椭圆的标准方程
(2)若![]() 求椭圆的离心率
求椭圆的离心率![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b是异面直线,给出下列结论:
①一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
③一定存在无数个平面![]() ,使直线b与平面
,使直线b与平面![]() 交于一个定点,且直线
交于一个定点,且直线![]() 平面
平面![]() .
.
则所有正确结论的序号为( )
A.②③B.①③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 与
与![]() 都为等边三角形,且侧面
都为等边三角形,且侧面![]() 与底面
与底面![]() 互相垂直,
互相垂直,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() 为棱
为棱![]() 上一点.
上一点.
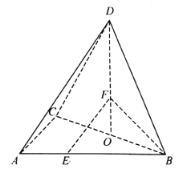
(1)试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)在(1)的条件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com