分析:(Ⅰ)要证明C1B⊥平面ABC,根据线面垂直的判定定理可知:需要证明C1B垂直于平面ABC内的两条相交直线即可.由已知AB⊥侧面BB1C1C,即可得到AB⊥BC1;在△CC1B中,先使用余弦定理求出BC1的长,进而再使用勾股定理得逆定理即可证得BC1⊥BC.
(Ⅱ)由于AB⊥侧面BB1C1C,要在线段CC1上找一点E,满足B1E⊥AE,根据三垂线定理,只要E点满足B1E⊥BE即可.若以线段BB1为直径画圆与线段CC1的交点(去掉点C、C1)即可满足要求.
解答:解:(I)证明:∵AB⊥侧面BB
1C
1C,∴AB⊥BC
1.
在△BC
1C中,BC=1,CC
1=BB
1=2,
∠BCC1=,
由余弦定理得
BC12=BC2+CC12-2BC•CC1COS=
12+22-2×1×2×=3,∴
BC1=.
故有BC
2+BC
21=CC
21,∴C
1B⊥BC,
而BC∩AB=B且AB,BC?平面ABC,
∴C
1B⊥平面ABC.
(II)如图所示:
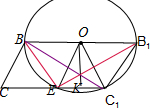
以线段BB
1为直径画圆O,分别交线段CC
1于点E、C
1.
下面说明点E、C
1是上述所画的圆与线段CC
1的交点.
①∵B
1C
1=OB
1=1,
∠OB1C1=,∴△OB
1C
1是正三角形,∴OC
1=1,即点C
1在所画的圆上.
②作OK⊥CC
1,垂足为K,取EK=KC
1,则点E也在所画的圆上.
∵OE=OC
1=1,∴点E也在所画的圆上.
∵CC
1∥BB
1,∴
∠OBE=∠OB1C1=,∴△OBE是正三角形,∴EB=1,
∴EB=BC=1,又∠BCE=
,∴△BCE为正三角形,∴CE=1,即E点是线段CC
1的中点.
下面证明点E满足条件.
∵AB⊥侧面BB
1C
1C,B
1E⊥BE,据三垂线定理可得B
1E⊥AE.
故线段CC
1的中点E即是要求的点.
点评:本题综合考查了线面垂直的判定定理和性质定理及三垂线定理,深刻理解以上定理是解决问题的关键.

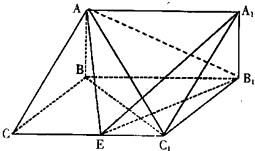 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,AB=
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,AB= 以线段BB1为直径画圆O,分别交线段CC1于点E、C1.
以线段BB1为直径画圆O,分别交线段CC1于点E、C1.

 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( ) 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.