
分析 由互斥事件的概率公式与独立事件的乘法公式计算可得答案.
解答 解:由题意,甲、乙、丙各自独立破译出密码的概率分别为$\frac{1}{5}$,$\frac{1}{4}$,$\frac{1}{3}$,
且他们是否破译出密码互不影响,
∴恰有二人破译出密码的概率为$\frac{1}{5}$×$\frac{1}{4}$×(1-$\frac{1}{3}$)+$\frac{1}{5}$×(1-$\frac{1}{4}$)×$\frac{1}{3}$+(1-$\frac{1}{5}$)×$\frac{1}{4}$×$\frac{1}{3}$=$\frac{3}{20}$.
故答案为:$\frac{3}{20}$.
点评 本题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题、解决问题的能力,难点在于对于恰有二人破译出密码的事件分类不清.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
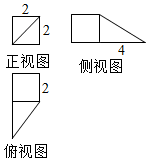
| A. | 28+4$\sqrt{5}$ | B. | 24+2$\sqrt{5}$ | C. | 18+4$\sqrt{5}$ | D. | 18+2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com