
| A. | 28+4$\sqrt{5}$ | B. | 24+2$\sqrt{5}$ | C. | 18+4$\sqrt{5}$ | D. | 18+2$\sqrt{5}$ |
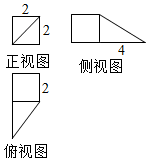
分析 根据三视图还原得到该几何体的直观图,即可得到结论.
解答 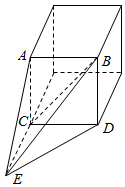 解:由三视图可知该几何体是正方体和四棱锥的组合体,
解:由三视图可知该几何体是正方体和四棱锥的组合体,
其中正方体的边长为2
四棱锥中CE=4,
则AE=DE=$\sqrt{4+16}=\sqrt{20}$=2$\sqrt{5}$,
则四棱锥的四个侧面面积S=S△ACE+S△CDE+S△ABE+S△BDE=$\frac{1}{2}×2×4$+$\frac{1}{2}×2×4$+$\frac{1}{2}×2\sqrt{5}×2$+$\frac{1}{2}×2\sqrt{5}×2$=4+4+2$\sqrt{5}$+2$\sqrt{5}$=8+4$\sqrt{5}$,
正方体5个面的面积S=5×2×2=20,
则组合体的表面积S=8+4$\sqrt{5}$+20=28+4$\sqrt{5}$,
故选:A
点评 本题主要考查三视图的应用,根据条件得到该几何体的直观图是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | [x]=|x| | B. | [x]≥$\sqrt{x^2}$ | C. | [x]>-x | D. | [x]>x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com