
分析 先画出图象设BP=1,则AP=2,CP=3,将△ABP绕B按顺时针旋转$\frac{π}{2}$到△CBE,判断边角关系以及求出PE和∠PEB,在△PEC中由余弦定理求出cos∠PEC,利用反三角函数表示出∠PEC,由角相等求出∠APB.
解答 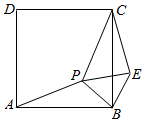 解:如图所示:由题意设BP=1,则AP=2,CP=3,
解:如图所示:由题意设BP=1,则AP=2,CP=3,
将△ABP绕B按顺时针旋转90°到△CBE,
∴BP=BE=1,∠APB=∠BEC,且∠PBE=90°,CE=AP=2,
则PE=$\sqrt{2}$,∠PEB=45°,
在△PEC中,由余弦定理得,
cos∠PEC=$\frac{P{E}^{2}+E{C}^{2}-P{C}^{2}}{2PE•EC}$=$\frac{2+4-9}{2×\sqrt{2}×2}$=$-\frac{3\sqrt{2}}{8}$,
∴∠PEC=arccos($-\frac{3\sqrt{2}}{8}$)
∴∠BEC=∠CEP+∠PEC=45°+arccos($-\frac{3\sqrt{2}}{8}$),
即∠APB=45°+arccos($-\frac{3\sqrt{2}}{8}$),
点评 本题考查余弦定理和反三角函数的应用,作辅助线是解题的关键,考查数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
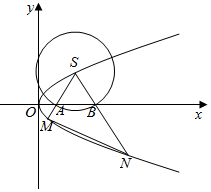 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.以S为圆心的动圆与x轴分别交于两点A、B,延长SA,SB分别交抛物线C于M,N两点.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.以S为圆心的动圆与x轴分别交于两点A、B,延长SA,SB分别交抛物线C于M,N两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com