
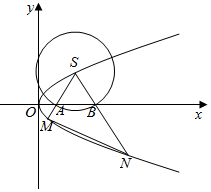
 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.以S为圆心的动圆与x轴分别交于两点A、B,延长SA,SB分别交抛物线C于M,N两点.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.以S为圆心的动圆与x轴分别交于两点A、B,延长SA,SB分别交抛物线C于M,N两点.分析 (1)设S(x0,y0)(y0>0),由已条件推导出|SF|=x0+$\frac{1}{4}$=$\frac{5}{4}$,由此能求出S点的坐标,再求出圆的半径,即可求圆S的方程;
(2)设直线SA的方程为y-1=k(x-1),M(x1,y1),由直线与抛物线方程联立,求出M点坐标,设直线SB的斜率为-k,同理求出N点坐标,由此能求出直线MN的斜率.
解答 解:(1)设S(x0,y0)(y0>0),
∵点F是抛物线C:y2=x的焦点,
S是抛物线C在第一象限内的点,且|SF|=$\frac{5}{4}$.
∴F($\frac{1}{4}$,0),∴|SF|=x0+$\frac{1}{4}$=$\frac{5}{4}$,
∴x0=1,∴y0=1
∴S点的坐标为(1,1).…(4分)
设圆S的半径为r,则$r=\sqrt{{1^2}+{{(\frac{1}{2}AB)}^2}}=\sqrt{2}$,
故圆S的方程为:(x-1)2+(y-1)2=2…(6分)
(2)设直线SA的方程为y-1=k(x-1)(k≠0),M(x1,y1),
由直线与抛物线方程联立,得ky2-y+1-k=0,
解得:y1=1(舍),或y1=$\frac{1}{k}$-1
∴M($\frac{(1-k)^{2}}{{k}^{2}}$,$\frac{1}{k}$-1)…(8分)
由已知|SA|=|SB|得,直线SA与SB的斜率互为相反数,
∴直线SB的斜率为-k,同理得N($\frac{(1+k)^{2}}{{k}^{2}}$,-$\frac{1}{k}$-1)…(10分)
∴kMN=$\frac{\frac{1}{k}-1+\frac{1}{k}+1}{\frac{(1-k)^{2}}{{k}^{2}}-\frac{(1+k)^{2}}{{k}^{2}}}$=-$\frac{1}{2}$,即直线MN的斜率为定值-$\frac{1}{2}$…(12分)
点评 本题主要考查抛物线上满足条件的点的坐标的求法,考查直线的斜率的求法,考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:填空题
 已知函数f(x)=Asin(ωx+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,且线段PQ的长与函数f(x)的周期相等,则函数f(x)的解析式为f(x)=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,且线段PQ的长与函数f(x)的周期相等,则函数f(x)的解析式为f(x)=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{6}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-x2 | B. | f(x)=$\frac{1}{{x}^{2}}$ | C. | f(x)=$\frac{1}{{x}^{3}}$ | D. | f(x)=x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com